 Hoci ešte nemáte k dispozícii matematický aparát na úplné pochopenie všetkých javov spojených so štatistickou fyzikou, jednoduchými programami niektoré javy môžete nasimulovať.
Hoci ešte nemáte k dispozícii matematický aparát na úplné pochopenie všetkých javov spojených so štatistickou fyzikou, jednoduchými programami niektoré javy môžete nasimulovať.
- Simulácia Rozloženie molekúl plynu v nádobe.
Skúsenosť nám hovorí, že ak máme nádobu, v jednej časti je vzduch a z druhej časti sme vzduch vyčerpali, ak prekážku medzi nimi odstránime, tlak vzduchu v oboch častiach nádoby sa vyrovná, v jednej i druhej nádobe bude rovnaké množstvo molekúl vzduchu. Ak by sme pustili film, ktorý zaznamenal priebeh expanzie plynu, tak by sme videli, ako sa rovnomerné rozloženie molekúl vzduchu zmení na stav prázdnej a plnej časti nádoby. Analýzou rýchlostí molekúl a ich polôh by sme zistili, že sa to neprieči fyzikálnym zákonom a bolo by to možné. Máme sa báť, že sa v miestnosti udusíme, lebo sa molekuly vzduchu môžu “rozhodnúť” premiestniť sa do opačného konca miestnosti? Prečo nepozorujeme, že by sa vyfúknutý balón sám od seba nafúkol?
Čo by program mal robiť?
Najprv sú všetky molekuly v ľavej časti nádoby, pridelíme im náhodné polohy a rýchlosti. Pohybujú sa len v ľavej časti nádoby. Odstránime prekážku (bola červená, bude zelená alebo celkom zmizne), molekuly sa začnú pohybovať v celej nádobe. Prvých 30 sekúnd nebudeme merať počet molekúl, potom raz za sekundu prípadne častejšie alebo menej často (príliš časté meranie by deformovalo štatistiku, lebo sa molekuly nestihnú premiestniť, takže merania by neboli nezávislé, príliš dlhé intervaly – nestihneme v rozumnom čase získať dostatočne veľký štatistický súbor), odmeriame, koľko molekúl je v ľavej časti nádoby. Histogram asi zobrazovať percentuálne, ale bol by tam aj počet nameraných hodnôt.
V tejto simulácii molekuly navzájom nebudú interagovať, pri náraze na stenu nádoby sa náhodne zmení zložka rýchlosti kolmá na stenu nádoby. Zdanlivé prechádzanie molekuly cez molekulu môžno vysvetliť tak, že vidíme dvojrozmerný priemet a molekuly sa minuli, jedna bola vpredu, druhá vzadu.
Parametre a funcionalita: Možnosť zvoliť koľko molekúl sa v nádobe nachádza. Vykresliť všetky mikrostavy do 6 molekúl.
Možnosť zastaviť priebeh simulácie. Vykresliť histogram počtu molekúl v ľavej časti nádoby, porovnať namerané hodnoty s teoretickými hodnotami. Predpokladáme, že molekuly možno navzájom rozlíšiť. Potom rozloženia (1|2) a (2|1) pokladáme za dva mikrostavy makrostavu jedna molekula je vľavo. Pre dve molekuly je pravdepodobnosť makrostavu jedna molekula je vľavo 50%, makrostav nádoba vľavo je prázdna má pravdepodobnosť 25% a sú v nej dve molekuly tiež 25%.
Pre 4 molekuly sú možné mikrostavy:
Makrostav 4, 1 mikrostav:(1234|)
Makrostav 3, 4 mikrostavy: (123|4) (124|3) (134|2) (234|1)
Makrostav 2, 6 mikrostavov: (12|34) (13|24) (14|32) (23|14) (24|13) (34|12)
Makrostav 1, 4 mikrostavy: (1|234) (2|134) (3|124) (4|123)
Makrostav 0, 1 mikrostav: (|1234)
Spolu je 16 možných mikrostavov. Počet mikrostavov je , kde
, kde 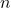 je počet molekúl.
je počet molekúl.
Vyvodiť záver na základe viacerých pokusov so 100 molekulami či viac molekulami. Uviesť tabuľku pre aspoň 5 simulácií a aspoň 1000 meraní.
Možno naprogramovať i zjednodušenú verziu programu, kde sa pre každú molekulu vygeneruje náhodné umiestnenie v nádobe a merať, ako často sa vyskytne ten či onen makrostav. Toto bude prebiehať výrazne rýchlejšie, ale nebude zrejmé, že sa molekuly aj hýbu. - Simulácia Rozloženie rýchlosti molekúl plynu
Na začiatku nech majú všetky molekuly rovnakú rýchlosť, ale každá sa pohybuje náhodným smerom. Uvažujme iba odpudivú silu medzi molekulami, ktorá nech je nepriamo úmerná druhej mocnine ich vzdialenosti, prípadne nájdete v literatúre vzťah, ktorý pre silu medzi nimi platí. Keď sú molekuly dostatočne ďaleko od seba, tak je sila medzi nimi pôsobiaca taká malá, že ju môžno zanedbať. Metódou pokusov a omylom prídete na to, od akej vzdialenosti môžno silu zanedbať.
Pre silu budeme mať dva vzťahy: a
a 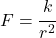 , tieto sily sú rovnaké, z veľkosti sily vypočítame aké zrýchlenie bude na molekulu pôsobiť. Pre rýchlosť po čase
, tieto sily sú rovnaké, z veľkosti sily vypočítame aké zrýchlenie bude na molekulu pôsobiť. Pre rýchlosť po čase  platí
platí 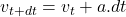
Vypočítame, aká výsledná sila na molekulu pôsobí, z toho vypočítame, aké bude mať zrýchlenie a zo zrýchlenia vypočítame novú rýchlosť molekuly, z novej rýchlosti vyrátame, kde sa bude nachádzať molekula po čase ,
,  musíme zvoliť dostatočne malé, inak by mohlo dôjsť k fyzikálne nereálnym javom (extrémny nárast rýchlosti, vzájomný preskok molekúl, nezachovávanie celkovej energie, …)
musíme zvoliť dostatočne malé, inak by mohlo dôjsť k fyzikálne nereálnym javom (extrémny nárast rýchlosti, vzájomný preskok molekúl, nezachovávanie celkovej energie, …)
Steny nádoby: Ak narazí molekula na stenu nádobu, jej rýchlosť v danom smere zmení znamienko. Nebudeme uvažovať o tom, že molekuly stien nádoby môžu molekulám plynu dodať alebo odobrať kinetickú energiu.
Parametre: počiatočná rýchlosť molekúl, počet molekúl, dráha konkrétnej molekuly, raz za 10 sekúnd alebo častejšie zaznamenáme rýchlosti všetkých molekúl, zvolíme si intervaly napríklad po 1 m za sekundu.
Po aspoň tisícke meraní porovnáme, či nami namerané hodnoty zodpovedajú Maxwell-Boltzmanovému rozdeleniu.
Uviesť tabuľku pre aspoň 5 meraní. Uviesť teoretický a nameraný graf.
Ak molekuly interagujú, zložitosť výpočtu rastie úmerne s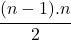 . Bude potrebné nájsť fintu, ako výpočtovú náročnosť minimalizovať, napríklad tak, že výpočet vzdialeností pre všetky molekuly budeme robiť v prvom kroku a potom v každom desiatom či dokonca 50 kroku. V medzičase budeme predpokladať, že sa nestihli k sebe natoľko priblížiť, aby sme silu medzi nimi nemohli zanedbať. Réžia na okresanie nesmie byť väčšia než by trval neorezaný výpočet. Vzdialenosť v trojrozmernom priestore vypočítame zo vzorca
. Bude potrebné nájsť fintu, ako výpočtovú náročnosť minimalizovať, napríklad tak, že výpočet vzdialeností pre všetky molekuly budeme robiť v prvom kroku a potom v každom desiatom či dokonca 50 kroku. V medzičase budeme predpokladať, že sa nestihli k sebe natoľko priblížiť, aby sme silu medzi nimi nemohli zanedbať. Réžia na okresanie nesmie byť väčšia než by trval neorezaný výpočet. Vzdialenosť v trojrozmernom priestore vypočítame zo vzorca  , kde
, kde  .
.
Pamäťové nároky: pre každú molekulu súradnice , rýchlosť
, rýchlosť 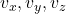 a zrýchlenie
a zrýchlenie 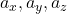 .
. - Simulácia Brownow pohyb.
Do peľového zrnka necháme narážať molekuly. Peľové zrnko bude mať 10000 krát väčšiu hmotnosť, ako molekuly, budeme zaznamenávať polohu peľového zrnka a budeme vykresľovať jeho dráhu. Hmotnosť peľového zrnka budeme môcť meniť. Budeme môcť meniť strednú kvadratickú rýchlosť molekúl respektíve teplotu kvapaliny. Zrážky budeme pokladať za dokonale pružné a povedieme ich tak, že stredy molekuly a peľového zrnka budú ležať na priamke rýchlosti, inak by sme museli uvažovať aj o rotácii, ktorú molekula zrnku udelí, rovnost uhlu odrazu a dopadu, … Ak toto bude zvládnuté, potom možno uvažovať o realistickejšom modely. Pre pružnú zrážku platí zákon zachovania energie a hybnosti. Ešte sme to nepreberali, vzorce sú: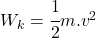 a
a 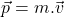 , kde
, kde 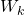 je kinetická energia a
je kinetická energia a 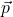 je hybnosť. Zrážky budeme pokladať za okamžité. Do peľového zrnka po náhodne zvolenom čase v náhodne zvolenom bode narazí molekula vody s náhodne zvolenou rýchlosťou, vypočítame, ako by sa zrnko pohlo.
je hybnosť. Zrážky budeme pokladať za okamžité. Do peľového zrnka po náhodne zvolenom čase v náhodne zvolenom bode narazí molekula vody s náhodne zvolenou rýchlosťou, vypočítame, ako by sa zrnko pohlo.
Priama zrážka dvoch dokonale pružných gúľ