Po otvorení súboru, klikni na Súbor a na stiahnuť. Stiahni wo formáte Microsoft Word. Po stiahnutí otvor stiahnutý súbor.
Matematika
Selfie
Meranie tepelnej kapacity kalorimetra
Ak tepelná výmena netrvá pridlho, stačí zistiť tepelnú kapacitu vnútornej nádoby. Kalorimeter, ak sme doň predtým nenaliali/nevyliali vodu, má rovnakú teplotu, ako je teplota miestnosti. Takže odmeriame teplotu miestnosti označme ju ![]() . Zohrejeme vodu a odmeriame jej teplotu. Označme ju
. Zohrejeme vodu a odmeriame jej teplotu. Označme ju ![]() . Odmeriame hmotnosť vody
. Odmeriame hmotnosť vody ![]() . Horúcu vodu nalejeme do kalorimetra a počkáme, kým sa teplota neustáli. Ustálenú teplotu označme
. Horúcu vodu nalejeme do kalorimetra a počkáme, kým sa teplota neustáli. Ustálenú teplotu označme ![]() .
.
Z kalorimetrickej rovnice plynie, že množstvo tepla, ktoré kalorimeter prijal sa rovná množstvu tepla, ktoré voda odovzdala.
Continue readingTepelná kapacita telesa
Tepelná kapacita telesa je množstvo tepla, ktoré je potrebné na zohriatie telesa o jeden stupeň celzia. Tepelnú kapacitu telesa označujeme veľkým ![]() . Pri rôznych teplotách je tepelná kapacita telesa rôzna, ak rozdiel teplôt nie je veľký, môžeme tepelnú kapacitu telesa pokladať za konštantnú.
. Pri rôznych teplotách je tepelná kapacita telesa rôzna, ak rozdiel teplôt nie je veľký, môžeme tepelnú kapacitu telesa pokladať za konštantnú.
Množstvo tepla, ktoré teleso prijme alebo odovzdá pri tepelnej výmene závisí od jeho tepelnej kapacity a rozdielu teplôt ![]() .
.
![]() , kde
, kde ![]() je pôvodná teplota telesa a
je pôvodná teplota telesa a ![]() je konečná teplota telesa.
je konečná teplota telesa.
![]()
Ak sa chceme vyhnúť záporným hodnotám tepla, môžeme v ![]() na prvé miesto dať vyššiu teplotu.
na prvé miesto dať vyššiu teplotu.
Tepelná kapacita telesa rastie s jeho hmotnosťou. Koľkokrát je hmotnosť telesa z tej istej látky väčšia, toľkokrát je väčšia jeho tepelná kapacita. Na základe toho môžeme zaviesť termín hmotnostná tepelná kapacita.
Hmotnostná tepelná kapacita látky je množstvo tepla potrebné na zohriatie 1 kg látky o jeden stupeň celzia. Označujeme ju malým ![]() . Hmotnostnú tepelnú kapacitu vypočítame zo vzorca:
. Hmotnostnú tepelnú kapacitu vypočítame zo vzorca:
![]() kde m je hmotnosť telesa.
kde m je hmotnosť telesa.
Hmotnostnú tepelnú kapacitu jednotlivých látok nájdeme v matematicko fyzikálno chemických tabuľkách. Môžeme ju tiež zistiť meraním a výpočtom z kalorimetrickej rovnice.
| Látka | Hmotnostná tepelná kapacita [c] |
| voda | 4180 |
| hliník | |
| meď | |
| železo | |
| olovo | |
| ľad | |
| vodík | |
| dusík | |
Piškvorky v Pythone
Piškvorky hrajú dvaja hráči proti sebe na štvorcovej sieti. Úlohou hráčov je vytvoriť za sebou 5 rovnakých symbolov vodorovne, zvislo alebo po diagonálach. Keď sa podarí projekt vytvoriť, pokúsime sa doplniť aj možnosť hrať proti počítaču.
Continue readingDotazník AI
GIF súbor
Pomocou ezgif sme vytvorili GIF súbor Samuela.

Zdieľanie súborov
Jukebox II.
V predchádzajúcom článku sme vytvorili prehrávač skladieb. Prehrávač bol funkčný, ale v časti prehrávania sa nám opakovali tie isté bloky. Keď sa v programe čosi také vyskytne, obvykle sa dá program zjednodušiť. Pridaním každej novej skladby musíme program upraviť na dvoch miestach: zmeniť počet skladieb a doplniť blok príkazov v bloku keď je logo stlačené.
Na zjednodušenie programu použijeme prvok pole. Pole je zoznam hodnôt. Čiže je to premenná, ktorá obsahuje viac hodnôt. Číslo skladby bude ukazovateľom na hodnotu v tomto poli.
V premenných vytvoríme premennú skladby. V rozšírené nájdeme kategóriu Polia. Zoberieme blok nastaviť zoznam na pole, zoznam zmeníme na skladby a do jednotlivých políčok poľa dáme skladby z play melody. Postupne tám dáme všetky preddefinované skladby. Časť nastavenia tohto poľa je vpravo

Zoznam všetkých deliteľov čísla
Úloha: Vypíš všetky delitele čísla 60.
Postup: Začneme jednotkou, potom skúšame dvojku, trojku … až kým nedôjdeme po číslo, ktorého súčin so sebou samým je väčší než skúmané číslo. Ďalej už nemá zmysel ísť, lebo čísla, ktoré by sme po delení dostali, by boli menšie, než toto hraničné číslo a tieto menšie čísla sme už otestovali.
Continue readingKritéria deliteľnosti
Deliteľnosť 2
Číslo je deliteľné 2, ak na mieste jednotiek je párna číslica: 0, 2, 4, 6, 8
Deliteľnosť 3
Číslo je deliteľné 3, ak jeho ciferný súčet (súčet jeho číslic) je deliteľný 3.
Príklad: 123 – 1+2+3=6, 6 je deliteľné 3, číslo 123 je deliteľné 3.
Deliteľnosť 4
Číslo je deliteľné 4, ak posledné dvojčíslie je deliteľné 4.
Deliteľnosť 5
Číslo je deliteľné 5, ak posledná číslica je 0 alebo 5.
Continue readingPomer, mierka, priama nepriama úmernosť. Príklady
- Uprav pomery na základný tvar:
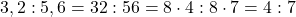
Priama úmernosť
Nech jeden rožok stojí 12 centov. V nasledujúcej tabuľke je cena nákupu v závislosti od počtu rožkov:
| ks | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| cena | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 |
Pre celkovú cenu za nákup platí vzorec: ![]() , kde c je cena a n je počet kusov.
, kde c je cena a n je počet kusov.
Priorita matematických operácií (Čo má prednosť?)
Tak ako v obyčajnom živote slušnosť káže dať prednosť pri vchádzaní do miestnosti alebo pri vychádzaní:
- žiak – učiteľovi
- mladší – staršiemu
- muž – žene
- podriadený – nadriadenému
aj pri počítaní matematických príkladov majú niektoré matematické operácie prednosť pred inými matematickými operáciami (majú vyššiu prioritu).
Continue readingPremeny stupňov na minúty a naopak
Jeden stupeň má 60 uhlových minút. ![]()
Jedna uhlová minúta má 60 uhlových sekúnd. ![]()
Potom jeden stupeň má 3600 sekúnd. ![]()
Keď premieňame stupne na minúty, počet stupňov vynásobíme 60.
Keď premieňame minúty na stupne, počet minút vydelíme 60. Ak nám zostane nejaký zvyšok, podiel napíšme v stupňov a zvyšok delenia v minútach.
![]()
![]()
![]()
![]()
Uhol
V aplikácii Microsoft Team v skupine Matematika 6 máte uloženú prezentáciu, ktorú som vám premietal počas online hodiny.

Uhol je časť roviny ohraničená dvoma polpriamkami, ktoré majú spoločný počiatok.
Polpriamky sa nazývajú ramená uhla.
Vrchol uhla je spoločný počiatok polpriamok.
Continue readingPrvočísla a zložené čísla
Dôkazy sú rozširujúcim a prehlbujúcim učivom, pre žiakov, ktorý sa hlbšie zaujímajú o matematiku. Nebudú predmetom skúšania.
| Číslo |
Aj číslo ![]() je deliteľom čísla
je deliteľom čísla ![]() , ak je
, ak je ![]() .
.
Možno to vyjadriť aj inak:
| Číslo |
Rozpíšme všetky možné vyjadrenia čísel od 1 do 20, ako súčinu dvoch čísel:
Zelenou farbou som označil čísla, ktoré majú iba dva delitele. Čiernou farbou sú napísané čísla, ktoré majú viac než dva delitele. Modrou farbou som označil číslo ![]() , ktoré má len jedného deliteľa.
, ktoré má len jedného deliteľa.
Prvočíslo je číslo, ktoré má dva delitele jednotku a samé seba.
Zložené číslo je číslo, ktoré má viac než dva delitele.
Veta: Číslo dva je jediné párne prvočíslo.
Dôkaz: Ak by číslo n bolo párne číslo väčšie ako dva, tak by malo delitele 1 a samé seba a navyše aj číslo 2.
Veta: Každé zložené číslo možno vyjadriť ako súčin prvočísel.
Dôkaz: Ak je n zložené číslo, možno ho vyjadriť ako súčin dvoch čísel väčších ako 1. ![]() . Tieto čísla sú buď prvočísla, alebo sú to znova zložené čísla. Ak sú to zložené čísla, možno ich vyjadriť ako
. Tieto čísla sú buď prvočísla, alebo sú to znova zložené čísla. Ak sú to zložené čísla, možno ich vyjadriť ako ![]() a
a ![]() . Tieto nové činitele sú aspoň dvakrát menšie, než pôvodné. Po konečnom počte krokov, dospejeme k číslu 2, ktoré je prvočíslom, alebo to už neboli zložené čísla.
. Tieto nové činitele sú aspoň dvakrát menšie, než pôvodné. Po konečnom počte krokov, dospejeme k číslu 2, ktoré je prvočíslom, alebo to už neboli zložené čísla.
Využitie prvočísel
- V súčasnosti sa prvočísla využívajú hlavne v kryptografii. Kryptografia je veda o šifrovaní a dešifrovaní. Ak máme zložené číslo, ktoré je súčinom dvoch veľmi veľkých prvočísel, dá sa správa zakódovať verejným kľúčom, ale dekódovať sa dá len súkromným kľúčom. Aj veľmi výkonné počítače pri dostatočnej veľkosti prvočísel by pracovali desiatky či stovky rokov, kým by odhalili súkromný kľúč.
- V informatike sa prvočísla používajú v hashovacích tabuľkách. Je to také ukladanie informácií, aby sme veľmi rýchlo našli informácie v databáze.
- V matematike možno pomocou prvočísel hľadať dokonalé čísla.
Dokonalé číslo je číslo, ktorého súčet vlastných deliteľov je rovný dokonalému číslu. Napríklad:
6 má vlastné delitele 1,2,3 a 6=1+2+3
28=1,2,4,7,14 a 28=1+2+4+7+14
Vlastný deliteľ je taký deliteľ, ktorý je menší než číslo ktoré delíme.
Starí Gréci prikladali dokonalým číslam magické vlastnosti.
Ovládanie korytnačky cez príkazový riadok
Po kliknutí na ikonu zelenej korytnačky sa spustí prostredie Imagine.
Hore sa zobrazí menu: Súbor Úpravy Ukázať Nastavenia Stránka Pomocník
Pod menu sú rôzne tlačítka. Ďalej nasleduje pracovná plocha, po ktorej sa pohybuje korytnačka (korytnačky).
Potom je pás, v ktorom je zoznam príkazov, ktoré sme korytnačke zadali a celkom dole je príkazový riadok, do ktorého zadávame príkazy korytnačke.
V tomto článku nájdete zoznam príkazov jazyka Imagine.
Sústava troch a viac lineárnych rovníc
Ak máme tri neznáme a všeobecne n neznámych, aby bolo riešenie jednoznačné, potrebujeme aspoň tri rovnice a všeobecne n rovníc. Ak máme tri neznáme, v matematike ich obvykle označíme písmenami x, y, z. Ak je neznámych viac, označujeme ich pomocou dolného indexu ![]() . Sústavu troch lineárnych rovníc riešime podobne, ako sústavu dvoch lineárnych rovníc substitučnou metódou.
. Sústavu troch lineárnych rovníc riešime podobne, ako sústavu dvoch lineárnych rovníc substitučnou metódou.
Sústava dvoch lineárnych rovníc o dvoch neznámych
Kedysi ste sa naučili riešiť lineárnu rovnicu s jednou neznámou. V živote či vo vede sa stretávame aj so zložitejšími problémami, keď neznáme môžu byť dve a viac. V tomto článku si ukážeme, ako možno riešiť sústavu dvoch lineárnych rovníc o dvoch neznámych. Prvú neznámu obvykle označíme x, druhú y, ale inak na označení nezáleží (vo fyzike ich napríklad označíme značkami fyzikálnych veličín).
Test množiny. Riešenia
Nižšie sú naskenované správne odpovede testu k množinám. Poradie otázok a odpovedí bolo u každého študenta individuálne. Prečo sú správne uvedené odpovede:
Exponenciálne rovnice
Exponenciálna funkcia so základom väčším ako 1 je rastúca a so základom menším ako 1 a väčším ako 0 je klesajúca. To znamená:
![]() . (1)
. (1)
alebo
![]() . (2)
. (2)
Túto vlastnosť využijeme pri riešení exponenciálnych rovníc.
Príklad 1: Vyriešte rovnicu ![]()
Pravú stranu upravíme na mocninu 5: ![]()
Pre ľavú stranu využijeme vzťah ![]() .
.
Dostaneme: ![]()
Teraz využijeme vzťah (1). Riešenie exponenciálnej rovnice sa zmení na riešenie lineárnej rovnice:
![]()
![]()
![]()
![]()
Skúška:
![]()
![]()
Skúška správnosti vyšla. Riešením rovnice je ![]() .
.
Zhrnutie riešenia: Ak na ľavej aj pravej strane máme mocniny s rovnakým základom, riešime rovnicu, v ktorej sa majú rovnať exponenty. Ak nemáme rovnaký základ, nájdeme spoločný základ mocniny. V tomto príklade spoločným základom bolo číslo 5.
Príklad 2: Vyriešte ![]()
Ako vyjadriť 0,125, ako mocninu nejakého čísla? Čo je spoločným základom? Môže to byť 4? ![]()
![]()
Zistili sme, že 4 to nie je. Číslo 4 je mocninou dvojky. ![]()
Pôvodnú rovnicu upravíme do tvaru:
![]()
Použijeme vzťah ![]() a dostaneme:
a dostaneme:
![]()
Teraz stačí vyriešiť lineárnu rovnicu, v ktorej sa exponenty majú rovnať.
![]()
![]()
![]()
![]()
Úlohy na riešenie:
- Tu pribudne niekoľko úloh
Zoom – online učebňa
Zoom je aplikácia, ktorá umožňuje spustiť videokonferenciu, v našich podmienkach online vyučovanie.
Látka z matematiky pre jednotlivé triedy
Kosínusová veta
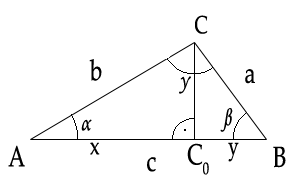
Majme trojuholník ABC, z vrcholu C veďme výšku na stranu c, ako ilustruje obrázok vpravo. Výška ![]() rozdelila trojuholník na dva pravouhlé trojuholníky
rozdelila trojuholník na dva pravouhlé trojuholníky ![]() a
a ![]() .
.
Pre oba trojuholníky platí Pytagorova veta:
![]()
![]()
![]()
![]()
![]()
![]()
Nepriama úmernosť
Jeden robotník vykope 20 metrový kanál za 8 hodín. Za koľko hodín ho vykopú dvaja robotníci, ak sú rovnako výkonní?
Dvaja robotníci kanál vykopú dvakrát rýchlejšie, takže ho vykopú za 4 hodiny.
Auto išlo priemernou rýchlosťou 60 km za hodinu, z obce Pršany do obce Dažďany došlo za 1 hodinu. Na bicykli cyklista dosahuje na tej istej trati rýchlosť 20 km za hodinu, ako dlho mu cesta potrvá?
Cyklista ide trikrát pomalšie, cesta mu bude trvať trikrát tak dlho. Trasu prejde za tri hodiny.
Oba vyššie uvedené príklady boli príklady nepriamej úmernosti.
Nepriama úmernosť medzi dvoma veličinami je, ak vzťah medzi nimi možno vyjadriť vzorcom: ![]() , kde k je konštanta úmernosti a
, kde k je konštanta úmernosti a ![]()
Priama úmernosť
Keď nakupujem rožky v obchode a jeden rožok stojí 8 centov, výsledná cena, ktorú zaplatím sa dá vyjadriť vzťahom: ![]() , kde c je cena a r je počet rožkov.
, kde c je cena a r je počet rožkov.
| Rožky | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Cena v centoch | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
Ak idem na bicykli konštantnou rýchlosťou 16 km za hodinu, dráha ktorú prejdem za nejaký čas sa dá vyjadriť vzťahom ![]() , kde s je dráha, a t je čas.
, kde s je dráha, a t je čas.
| Čas | 0 min | 15 min | 30 min | 1 hod | 2 hod | 3 hod |
| Dráha | 0 km | 4 km | 8 km | 16 km | 32 km | 48 km |
Poznámka: 15 minút je štvrť hodiny.
Hore uvedené vzťahy boli príklady priamej úmernosti.
Priama úmernosť medzi dvoma veličinami je, ak hodnotu závislej premennej od nezávislej premennej možno vyjadriť vzorcom v tvare: ![]() , kde
, kde ![]() . Konštanta priamej úmernosti k, je kladné reálne číslo.
. Konštanta priamej úmernosti k, je kladné reálne číslo.
Základné pojmy pravdepodobnosti
Majme stanovený systém podmienok (napr. máme pravidelnú hraciu kocku, ktorej steny sú označené číslami 1, 2, . . . , 6). Proces (dej), ktorý môže nastať pri realizácii týchto podmienok (napr. hod hracou kockou) nazývame pokus. Vyžadujeme, aby každý pokus mal vlastnosť hromadnosti, t. j. aby sme ho mohli teoreticky ľubovoľne krát opakovať. Výsledok tohto procesu nie je jednoznačný, je náhodný, nazývame ho náhodným javom alebo náhodnou udalosťou (napr. padnutie šestky). Náhodný jav je výsledok pokusu. Množinu všetkých navzájom sa vylučujúcich výsledkov pokusu označujme gréckym písmenom ![]() . Jej prvky nazývame elementárne udalosti a označujeme ich písmenom
. Jej prvky nazývame elementárne udalosti a označujeme ich písmenom ![]() , t.j.
, t.j. ![]() . Podmnožiny množiny všetkých možných výsledkov pokusu nazývame náhodnými udalosťami.
. Podmnožiny množiny všetkých možných výsledkov pokusu nazývame náhodnými udalosťami.
Náhoda a pravdepodobnosť
Niektoré javy sú také, že vieme dopredu s absolútnou istotou povedať, čo sa stane za daných okolností:
- ak zdvihneme teleso a pustíme ho, vieme že spadne na zem
- ak priblížime k sebe dva magnety, začnú sa priťahovať alebo odpudzovať, podľa toho, ktoré póly magnetov sú bližšie k sebe
- ak voda dosiahne 100 stupňov celzia pri normálnom tlaku, začne vrieť
- ak teplota klesne pod 0 stupňov celzia pri normálnom tlaku, zmrzne
Iné javy sú také, že nevieme s istotou povedať čo nastane, ale vieme že nastane niektorá z možností:
- hodíme kocku, padne jedno z čísel 1, 2, 3, 4, 5, 6, ale dopredu nevieme, ktoré z nich to bude
- hodíme mincu, padne rub alebo líc
- meteorológovia namerajú údaje v atmosfére a síce predpovedia, aké bude počasie, ale čas od času im predpoveď nevyjde
- voda síce pri 100 stupňoch celzia začne vrieť, ale nevieme dopredu povedať, či konkrétna molekula vody bude ešte v hrnci o 5 sekúnd
Prvú triedu nazývame deterministické javy. Druhú triedu javov nazývame náhodné javy.
Precenenie tovaru
V praxi neraz budete tovar preceňovať. Buď ho o nejaké percentá zdražíte alebo zlacníte, alebo zmenu vypočítate pripočítaním alebo odpočítaním nejakej čiastky a spätne budete potrebovať zistiť o koľko percent ste cenu zvýšili alebo znížili.
Zlacnenie: Ak tovar chceme zlacniť o p%, novú cenu vypočítame zo vzorca: ![]() kde
kde ![]() je nová cena a
je nová cena a ![]() je pôvodná cena.
je pôvodná cena.
Príklad: Tovar stoji 70 euro, zlacníme ho 20%. Aká bude nová cena?![]()
Nová cena bude 56 euro.
Zdraženie: Ak tovar chceme zdražiť o p%, novú cenu vypočítame zo vzorca ![]() kde
kde ![]() je nová cena a
je nová cena a ![]() je pôvodná cena.
je pôvodná cena.
Dotazník pre štatistický prieskum
Kliknite na tento odkaz a vyplňte dotazník
Neskôr tu pribudne štatistické vyhodnotenie
Goniometrické funkcie
Ešte na základnej škole ste sa učili o podobnosti trojuholníkov.
Dva trojuholníky ![]() sú podobné ak platí:
sú podobné ak platí: ![]()
Konštantu k nazývame koeficient podobnosti. Ak je k väčšie ako 1, trojuholník sme zväčšili, ak je menšie ako 1 zmenšili a ak je rovný 1, trojuholníky sú zhodné.
Učili ste sa tiež vetu UU.
Veta UU: Ak sú v dvoch trojuholníkoch dva uhly zhodné, potom sú trojuholníky podobné.
Zároveň vieme, že súčet vnútorných uhlov trojuholníka je ![]() .
.
Z uvedených znalostí možno odvodiť, že ak máme dva pravouhlé trojuholníky a jeden z ostrých uhlov jedného trojuholníka je zhodný s ostrým uhlom v druhom trojuholníku, potom sú trojuholníky podobné, pretože majú dva zhodné uhly.
Z toho vyplýva, že pomer strán pravouhlých trojuholníkov s rovnakými uhlami je rovnaký a môžeme zaviesť funkcie uhlov, ktoré budú odvodené z pomerov strán pravouhlého trojuholníka:
![]()
Radián
Na základnej škole ste veľkosť uhla merali v stupňoch, kde celý kruh mal 360 stupňov, pravý uhol mal 90 stupňov, rovnostranný trojuholník mal 60 stupňové uhly, …
Rozdelenie kruhu na 360 stupňov zaviedli už Babylončania. Vo fyzike sa ukázalo užitočné merať uhly v radiánoch.

Radián je uhol, ktorý s vrcholom v strede kružnice vytne na kružnici oblúk s dĺžkou rovnou dĺžke polomeru. Značka rad.
Obvod kruhu počítame podľa vzorca: ![]() , potom 360 stupňom zodpovedá
, potom 360 stupňom zodpovedá ![]()
![]()
| Stupne | Radiány |
| 0 | |
| 30 | |
| 45 | |
| 60 | |
| 90 | |
| 120 | |
| 180 | |
| 270 | |
| 360 | |
Riešenia percentá
- Koľko percent je 30 zo 120?
- Koľko percent je 25 z 80?
- Koľko percent je 15 zo 40?
- Koľko percent je 8 z 24?
- Ak je základ 400, koľko je 25%?
- z=400, p=25, c =?
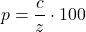
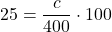
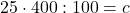
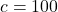
- 25 % zo 400 je 100
- Ak je základ 280, koľko je 30%?
- 100% ….. 280
- 1% ………..2,8
- 30% ………30 x 2,8= 84
- 30% z 280 je 84
- Ak je základ 90, koľko je 47%?
- 100% ………. 90
- 1% …………… 0,9
- 47% …………47 x 0,9=42,3
- 47% z 90 je 42,3
- Ak je základ 333, koľko je 50%?
- 50% je polovica, 333:2=166,5
- 50% z 333 je 166,5
- Ak je 10% 7, koľko je základ?
-
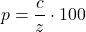
- z= \dfrac{c}{p}\cdot 100
- z= \dfrac{7}{10}\cdot 100=70
- Ak je 10% 7, potom je základ 70 .
-
- Ak je 33% 99, koľko je základ?
- 33% ………. 99
- 1 % ……….. 99:33=3
- 100% ……..3.100=300
- Ak je 33% 99, základ je 300.
- Ak je 75% 90, koľko je základ?
- 75% …… 90
- 1% ……… 90:75=1,2
- 100% ….. 1,2 x 100=120
- Ak je 75% 90, základ je 120.
- Ak je 13% 26, koľko je základ?
- 13% ……… 26
- 1% ……….. 26:13=2
- 100% ……. 2 x 100=200
- Ak je 13% 26, základ je 200.
- Po zlacnení o 20% televízor stoji 400 euro. Koľko stál pred zlacnením?
- Ak televízor zlacnel o 20%, jeho aktuálna cena je 80% pôvodnej ceny.
- 80%……400
- 1% ……..400:80=5
- 100%…..5 x 100=500
- Televízor pred zlacnením stál 500 euro.
- Po zlacnení o 25% stojí práčka 300 euro. Koľko stála pred zlacnením?
- 100-25=75. Aktuálna cena je 75% pôvodnej ceny.
- 75%…….300
- 1%……….300:75=4
- 100%…..4.100=400
- Po zdražení o 10% stojí auto 7700 euro. Koľko stálo pôvodne?
- 100+10=110. Nová cena je 110% p;vodnej ceny.
- 110%……7700
- 1%………..7700:110=70
- 100%……70.100=7000
- Pred zdražením stál lístok MHD 60 centov, po zdražení stojí 90 centov. Koľko percentné zdraženie to bolo?
- 100%…….60
- 1%………..60:100=0,6
- zdraženie je 90-60=30
- 30:0,6=50
- Zdraženie lístkov bolo 50%.
- Mesačník na MHD stál 20 euro, po zdražení stojí 25 euro. Koľko percentné zdraženie to bolo?
- 100%…………20
- 1%…………….0,20
- zdraženie 25-20=5
- 5:0,2=25
- Zdraženie mesačníkov bolo 25%.
- Pred zdražením som jazdil mesačne priemerne 25 krát s MHD, teraz jazdím o 40% menej často. O koľko odo mňa získa na tržbách dopravný podnik viac alebo menej za celý rok oproti minulosti?
- Rok má 12 mesiacov, pôvodne som minul 12.25.0,6=180 euro
- 25.0,6=15 jázd mesačne po zdražení
- ročne 12.15.0,9=162 euro
- 180-162=18
- Dopravný podnik odo mňa získa ročne o 18 euro menej ako pred zdražením.
Percentá
Neraz sa stáva, že potrebujeme porovnať dva či viac objektov rovnakého druhu z hľadiska ich štruktúry, pričom objekty nie sú rovnako veľké. Majme dve školy, na jednu chodí 400 žiakov z toho 100 dievčat, na druhú 600 žiakov z toho 120 dievčat. Hoci na druhú školu chodí v absolútnej hodnote dievčat viac, relatívne ich tam chodí menej. Relatívny počet dievčat na oboch školách možno vyjadriť zlomkami:
![]() a
a ![]()
Keď porovnávame relatívne počty, stalo sa zvykom, že relatívny počet prevedieme na zlomok s menovateľom 100 a aby sme nemuseli písať zlomok píšeme znak %.
Hore uvedené zlomky potom prejdú do tvaru ![]() a
a ![]() .
.
Znak % čítame ako percento, názov pochádza z latinského per cento znamenajúce na sto podobne ako jeden cent je stotina eura.
Pascalov trojuholník
Hoci sa Pascalov trojuholník nazýva podľa matematika Blaise Pascala, neobjavil ho on, ale poznali ho už v 13. storočí čínski matematici. Pascal však tento trojuholník a vzťahy ktoré v ňom platia preštudoval do hĺbky a tak bol pomenovaný po ňom.
Ako vytvoríme Pascalov trojuholník?
Do nultého riadku napíšeme 1, do prvého dve jednotky tak, že jednotka z predchádzajúceho riadku je v strede medzi nimi. Na začiatok a koniec každého ďalšieho riadku napíšeme jednotku a na ostatné pozície napíšeme súčet čísel, ktoré sú nad ním vľavo a vpravo. Tak ako ukazuje animovaný obrázok:

Možno dokázať, že jednotlivé čísla Pascalovho trojuholníka zodpovedajú kombinačným číslam.
| n | | |||||||||||
| 0 | | | ||||||||||
| n=1 | | | | |||||||||
| n=2 | | | | | ||||||||
| n=3 | | | | | | |||||||
| n=4 | | | | | | | ||||||
| n=5 | | | | | | | |

Vlastnosti Pascalovho trojuholníka
- Pascalov trojuholník je osovo súmerný podľa osi prechádzajúcej horným vrcholom.
- Súčet čísel v každom riadku zodpovedá n-tej mocnine čísla 2.
-
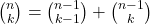 pre
pre 
Kombinačné čísla
Počet kombinácií bez opakovania sme vyjadrili vzorcom:
![]()
Kombinačné číslo zapisujeme ako ![]() , čítame ako n nad k a jeho hodnotu vypočítame rovnako ako počet kombinácií bez opakovania:
, čítame ako n nad k a jeho hodnotu vypočítame rovnako ako počet kombinácií bez opakovania: ![]()
Kombinačné čísla sa vyskytujú nielen v kombinatorike, ale aj pri iných matematických úlohách. Napríklad koeficienty pri rozpísaní mocniny ![]() usporiadané zostupne podľa exponentov pri a.
usporiadané zostupne podľa exponentov pri a.
Štatistické charakteristiky
Štatistické charakteristiky sú hodnoty, ktoré charakterizujú štatistický súbor ako celok. Medzi štatistické charakteristiky patria:
- aritmetický priemer
- geometrický priemer
- kvadratický priemer
- harmonický priemer
- medián
- modus
- smerodajná odchýlka
- rozptyl
- korelácia
Štatistika
Štatistika alebo matematická štatistika je odbor matematiky, ktorý skúma štatistické súbory – súbory štatistických jednotiek. Zosumarizujú sa znaky jednotlivých jednotiek a potom sa vyhodnotia charakteristické znaky celého štatistického súboru.
Štatistika úzko súvisí s pravdepodobnosťou. Niekedy môžeme preskúmať iba časť celku, vyhodnotením štatistických charakteristík tejto časti vieme s istou spoľahlivosťou určiť charakteristiky celého súboru.
Základné pojmy štatistiky
Štatistický súbor je súbor štatistických jednotiek s nejakou spoločnou vlastnosťou.
Štatistická jednotka je prvok štatistického súboru, jednotlivý objekt štatistického skúmania: osoba pri sčítaní obyvateľstva; častica pri skúmaní vlastností plynov, kvapalín; domácnosť pri výskume vybavenosti domácností…
Rozsah štatistického súboru je počet štatistických jednotiek v štatistickom súbore, ![]() .
.
Kvadratická rovnica
Kvadratická rovnica je rovnica, ktorú možno previesť na tvar:
![]() kde
kde ![]()
![]() – kvadratický člen
– kvadratický člen
![]() – lineárny člen
– lineárny člen
![]() – absolútny člen
– absolútny člen
Kvantifikátory
Niektoré výroky obsahujú slová každý, všetci, existuje, …
Každý a všetci neznamená to isté. Výroky:
Každý žiak triedy dostal z písomky jednotku.
Všetci žiaci triedy dostali z písomky jednotku.
sú ekvivalentné, ale napríklad výroky
Každý človek sa zmestí do tejto skrine.
Všetci ľudia sa zmestia do tejto skrine.
ekvivalentné nie sú. Z uvedeného vidno, že hovorová reč často nie je presná, máme v druhom výroku na mysli všetci súčasne alebo osobitne ako v prvom výroku?
Poznámka: Jeden zo žiakov uviedol iný príklad, kedy slovo každý nemožno nahradiť slovom všetci: Každý druhý.
Všeobecný kvantifikátor: Slovo každý(-á,-é) v matematike vyjadrujeme symbolom ![]() . Tento symbol nazývame všeobecný kvantifikátor.
. Tento symbol nazývame všeobecný kvantifikátor.
Existenčný kvantifikátor: Slovo existuje v matematike vyjadrujem symbolom ![]() . Tento symbol nazývame existenčný kvantifikátor.
. Tento symbol nazývame existenčný kvantifikátor.
Riešenia (lineárne rovnice)
Vyriešte rovnice a vykonajte skúšku správnosti

a) ![]()
![]()
![]()
Skúška: ![]()
b) ![]()
![]()
![]()
Skúška: ![]()
c) ![]()
![]()
![]()
![]()
Lineárna rovnica
Lineárna rovnica je každá rovnica, ktorú môžeme „korektnými“ úpravami previesť na tvar: ![]()
kde ![]() .
.
„Korektné“ úpravy sú také úpravy, ktoré nezmenia riešenie rovnice. Úpravy ktoré nemenia riešenie rovnice nazývame ekvivalentné úpravy.
ekvivalentný – majúci rovnakú cenu, hodnotu, rovnocenná náhrada
Graf funkcie
Aký má funkcia priebeh najlepšie uvidíme, ak nakreslíme jej graf.
Najprv nakreslíme súradnicové osy x a y a zvolíme veľkosť jednotkovej úsečky. Obvykle volíme rovnaké jednotkové úsečky pre os x aj y, ale ak funkcia prudko rastie alebo klesá, či naopak, y hodnoty budú v absolútnej hodnote výrazne menšie než hodnoty x môžeme zvoliť rôzne jednotkové úsečky.
Potom si vytvoríme tabuľku, do ktorej zapíšeme hodnoty x do prvého riadku a hodnoty y do druhého riadku. Ak by sme mali napríklad funkciu f(x)=x 2, mohla by tabuľka vyzerať takto:
| x | -4 | -3 | -2 | -1 | -0,5 | 0 | 0,5 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0,25 | 0 | 0,25 | 1 | 4 | 9 | 16 |
Vedieme kolmice na os x v bodoch z prvého riadku a kolmice na os y v bodoch druhého riadku, kde sa tieto kolmice pretnú, označíme bod krúžkom. Keď sme vyznačili všetky body z tabuľky, prepojíme ich krivkou.
Kombinácie
Príklad 1: Trieda má 20 žiakov, koľkými spôsobmi z nich možno vytvoriť týždenníkov.
Riešenie: Prvého týždenníka môžeme vybrať z 20 možností a druhého z 19, ale u týždenníkov neurčujeme, ktorý z nich je prvý alebo druhý týždenník, takže ak ako prvého týždenníka zvolíme pôvodne druhého týždenníka a naopak, je to stále tá istá voľba, takže Súčin 20 krát 19 musíme predeliť dvoma. Celkový počet možností je teda 190.
Príklad 2: V hre loto sa žrebuje 6 čísel plus dodatkové číslo zo 49 čísel. Aká je pravdepodobnosť, že hráč vyhrá jackpot, ak podal jeden tip?
Než budeme riešiť druhý príklad, zadefinujeme, čo je to kombinácia.
Kombinácia k-tej triedy z n-prvkov bez opakovania je výber k prvkov z n-prvkovej množiny, pričom nezáleží na poradí prvkov a prvky sa neopakujú.
Riešenia (permutácie s opakovaním)
Úlohy
- Koľko permutácií s opakovaním možno vytvoriť z písmen slova OKOLO?
- V krabičke je 10 farbičiek: 4 červené, 3 modré, 2 žlté a jedna zelená. Koľkými spôsobmi ich môžeme usporiadať, ak farbičky rovnakej farby nevieme rozlíšiť?
- Osem študentov sa môže ubytovať v troch izbách, pričom dve sú trojposteľové a jedna dvojposteľové. Koľkými spôsobmi sa môžu študenti ubytovať?
- Šesťciferný kód na trezore sa skladá z rovnakých číslic ako číslo 926002 a zlodej to vie. Ako najdlhšie by zlodejovi trvalo, než by trezor otvoril, ak nastavenie jednej kombinácie číslic trvá 5 sekúnd?
- Koľko rôznych aj bezvýznamových slov možno zostaviť zo slova MATEMATIKA, ak sa použijú všetky písmená?
Permutácie
Permutácia je usporiadanie všetkých prvkov množiny.
Permutácia je špeciálny prípad variácie. Je to variácia n-tej triedy z n prvkovej množiny. Ak sa prvky v množine neopakujú:
![]()
Počet permutácií n-prvkovej množiny bez opakovania teda je: ![]()
Variácie
Príklad: Šachového turnaja sa zúčastnilo 8 hráčov. Koľko rôznych umiestnení mohlo byť na prvých troch miestach?
Riešenie: Na prvom mieste mohlo byť 8 hráčov, ak už na prvom mieste máme hráča, na druhom môže byť 7 hráčov a na treťom už len 6, lebo dvaja už sú na prvom a druhom. Počet možných umiestnení na prvých troch miestach je teda 8.7.6=336.
Príklad: Trieda má 20 žiakov. Žiaci si idú voliť triedny výbor: predsedu, podpredsedu a pokladníka. Koľko rôznych zostáv môže mať výbor triedy.
Riešenie: Za predsedu môže byť zvolených 20 žiakov, za podpredsedu už len 19, lebo predseda nemôže byť aj podpredsedom a za pokladníka 18, lebo pokladník nemôže byť zároveň predsedom alebo podpredsedom. Počet rôznych zostáv výboru je 20.19.18=6840.
Oba vyššie uvedené príklady boli príkladmi variácií bez opakovania, keď každý prvok sa vo výbere mohol vyskytnúť iba raz a záležalo na poradí prvkov.
Variácia k-tej triedy z n prvkovej množiny je výber k prvkov z n prvkov.
Ak sa prvky nemôžu opakovať, je to variácia bez opakovania.
Ak sa prvky opakovať môžu, je to variácia s opakovaním.
Kombinatorika
Kombinatorika je matematická disciplína, ktorá sa zaoberá kombinovaním rôznych súborov objektov. Napr. Koľko je možných rôznych poradí na prvých troch miestach, ak je súťažiacich 10? Aká je pravdepodobnosť jackpotu v lotte? Ako spravodlivo nasadiť družstvá v turnaji? Ako zostaviť rozvrh školy, aby vyhovoval daným kritériám?
Výsledky kombinatoriky sa využívajú napríklad pri výpočtoch pravdepodobnosti.
Príklad: Koľko existuje dvojciferných čísel, v ktorých sa číslice neopakujú?
Funkcia
Funkcia na množine D je ľubovoľný predpis, ktorý každému prvku množiny D priradí práve jedno reálne číslo. Funkciu označujeme malým písmenom.
Prvky množiny D nazývame nezávislá premenná, ich obrazy sú závislá premenná. Nezávislú premennú obvykle označujeme x a závislú y, ale môžeme zvoliť také označenie, aby bolo zrejmé čo tieto premenné označujú. napríklad ![]() , kde
, kde ![]() je dráha,
je dráha, ![]() je konštantná alebo priemerná rýchlosť a
je konštantná alebo priemerná rýchlosť a ![]() je čas.
je čas.
