Úlohy
- Koľko permutácií s opakovaním možno vytvoriť z písmen slova OKOLO?
- V krabičke je 10 farbičiek: 4 červené, 3 modré, 2 žlté a jedna zelená. Koľkými spôsobmi ich môžeme usporiadať, ak farbičky rovnakej farby nevieme rozlíšiť?
- Osem študentov sa môže ubytovať v troch izbách, pričom dve sú trojposteľové a jedna dvojposteľové. Koľkými spôsobmi sa môžu študenti ubytovať?
- Šesťciferný kód na trezore sa skladá z rovnakých číslic ako číslo 926002 a zlodej to vie. Ako najdlhšie by zlodejovi trvalo, než by trezor otvoril, ak nastavenie jednej kombinácie číslic trvá 5 sekúnd?
- Koľko rôznych aj bezvýznamových slov možno zostaviť zo slova MATEMATIKA, ak sa použijú všetky písmená?
- O sa opakuje 3 krát, K a L raz.
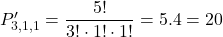
Zo slova OKOLO môžene vytvoriť 20 permutácií s opakovaním. 
Farbičky môžeme usporiadať 12600 spôsobmi.- Keďže nás nezaujíma, ktorý študent spí na ktorej posteli ale iba na ktorej izbe, na postele v rovnakej izbe sa môžeme dívať ako na rovnaké objekty. Potom počet permutácií s opakovaním je:
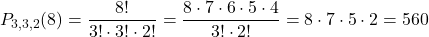
Existuje 560 možností rozdelenia študentov do izieb. - 9 a 6 sú raz, 2 a 0 dvakrát. Počet kombinácií s opakovaním je:
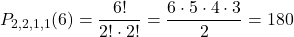
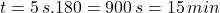
Zlodejovi by trvalo najviac 15 minút, než by otvoril trezor. - V slove MATEMATIKA sa 3x vyskytuje A, 2x M a T 1x E,I,K.

Slov, ktoré možno vytvoriť zo všetkých písmen slova matematika je 151200.
One Comment