Variácie

Príklad: Šachového turnaja sa zúčastnilo 8 hráčov. Koľko rôznych umiestnení mohlo byť na prvých troch miestach?

Riešenie: Na prvom mieste mohlo byť 8 hráčov, ak už na prvom mieste máme hráča, na druhom môže byť 7 hráčov a na treťom už len 6, lebo dvaja už sú na prvom a druhom. Počet možných umiestnení na prvých troch miestach je teda 8.7.6=336.

Príklad: Trieda má 20 žiakov. Žiaci si idú voliť triedny výbor: predsedu, podpredsedu a pokladníka. Koľko rôznych zostáv môže mať výbor triedy.

Riešenie: Za predsedu môže byť zvolených 20 žiakov, za podpredsedu už len 19, lebo predseda nemôže byť aj podpredsedom a za pokladníka 18, lebo pokladník nemôže byť zároveň predsedom alebo podpredsedom. Počet rôznych zostáv výboru je 20.19.18=6840.

Oba vyššie uvedené príklady boli príkladmi variácií bez opakovania, keď každý prvok sa vo výbere mohol vyskytnúť iba raz a záležalo na poradí prvkov.

Variácia k-tej triedy z n prvkovej množiny je výber k prvkov z n prvkov.

Ak sa prvky nemôžu opakovať, je to variácia bez opakovania.

Ak sa prvky opakovať môžu, je to variácia s opakovaním.

Koľko je variácii bez opakovania?

Postupujeme ako v hore uvedených príkladoch: prvý prvok môžeme zvoliť ľubovoľne, čiže máme n možností, druhý prvok vyberáme z n-1 prvkovej množiny, ďalší z n-2 prvkovej a takto pokračujeme až po k-tý prvok, ktorý vyberáme z n+1-k prvkovej množiny. Označme počet variácii k-tej triedy z n prvkov $V_k(n)$ . Potom platí: $V_k(n)=\dfrac{n!}{(n-k)!}$

Je to súčin: $n\cdot (n-1) \cdot (n-2) ... (n+1-k)$

Koľko je variácii s opakovaním?

Vyberáme v každom kroku z n prvkovej množiny, počet variácií s opakovaním je potom: $V_k' (n)=n^k$

Úlohy

Ak sa zväčší počet prvkov o dva, počet variácií tretej triedy bez opakovania sa zväčší o 384. Aký je počet prvkov?
Vo vrecku je 6 lístkov s číslami od 1 do 6. Koľkými spôsobmi môžeme vytiahnuť tri lístky, ak lístky do vrecka nevraciame?
Počet trojčlenných variácií bez opakovania je 10 násobok počtu dvojčlenných variácií bez opakovania. Koľko prvkov má množina?
V slovenskej hokejovej lige hrá 10 družstiev. Koľkými spôsobmi môžu byť rozdelené medaily (zlaté, strieborné a bronzové)?
O telefónnom čísle svojho spolužiaka Peter vedel: je 6-miestne, začína sedmičkou, žiadna číslica sa neopakuje, je deliteľné 25. Koľko čísel môže vyskúšať?

Riešenia:

$V_3(n+2)-V_3(n)=384$

$\dfrac{(n+2)!}{(n+2-3)!}-\dfrac{n!}{(n-3)!}=(n+2)\cdot (n+1) \cdot n - n \cdot (n-1) \cdot (n-2)=384$

$6n^2=384\, / :6$
$n^2=64,\ / \sqrt$
$n=8$
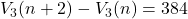
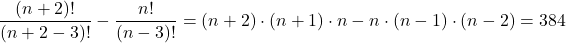
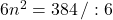
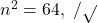
Skúška: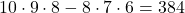 $10 \cdot 9 \cdot 8 - 8\cdot 7 \cdot 6=384$
Počet prvkov je 8
$V_3(6)=\dfrac{6!}{(6-3)!}=6\cdot 5 \cdot 4=120$
Lístky môžeme vytiahnuť 120 spôsobmi.
$V_3(n)=10\cdot V_2(n)$
$\dfrac{n!}{(n-3)!}=10 \cdot \dfrac{n!}{(n-2)!}$
$n\cdot (n-1) \cdot (n-2)=10 \cdot n \cdot (n-1) / :n:(n-1)$
$n-2=10 / +2$
$n=12$
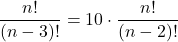
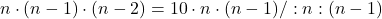
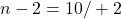
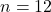
Skúška: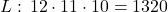 $L:\, 12 \cdot 11 \cdot 10=1320$
$P:\, 10 \cdot 12 \cdot 11=1320$
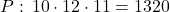
Množina má 12 prvkov.
Ide o variácie tretej triedy z 10 prvkov bez opakovania.
$V_3(10)=\dfrac{10!}{(10-3)!}=10 \cdot 9 \cdot 8= 720$
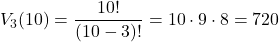
Medaily možno rozdeli 720 spôsobmi.
Na prvom mieste nemôže byť nula na posledných dvoch bude 25, 50. Ak je na konci 25, na 2. miesto môže ísť 7 číslic, na tretie 6, na štvrté 5.. To isté ak je na konci 50.
$2 \cdot (7.6.5)=420$
Peter môže vyskúšať 420 možností.

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Pridaj komentár Zrušiť odpoveď