Riešené príklady na výkon a prácu

Pri počítaní príkladov na výkon využijeme všetky vzorce, ktoré sme preberali v súvislosti s prácou, silou, trením, gravitačnou silou, … Základné vzorce:

gravitačná sila $F_g=m.g$
gravitačné zrýchlenie $g=10\cfrac{N}{kg}$
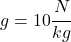
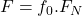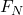statické trenie $F=f_0.F_N$ , kde $F_N$ je sila pôsobiaca kolmo na podložku, 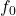$f_0$ je koeficient statického trenia
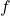dynamické trenie $F=f.F_N$ , kde $f$ je koeficient dynamického trenia
mechanická práca 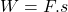$W=F.s$ , ak sila a smer pohybu sú rovnobežné, inak silu musíme rozložiť na zložku pôsobiacu v smere pohybu a na zložku kolmú na tento pohyb.
výkon $P=\cfrac{W}{t}$

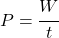
Vzpierač zdvihol činku s hmotnosťou 90 kg do výšky 2,5 m za 3 sekundy. Aký pritom podával priemerný výkon?
Zápis:
m=90 kg
h=2,5 m
t=3 s
P=?
Riešenie:
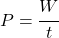$P=\cfrac{W}{t}$ (výkon)
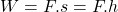$W=F.s=F.h$ (práca)
$F=m.g$ (gravitačná sila)
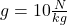$g=10\frac{N}{kg}$ (gravitačné zrýchlenie) 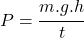$P=\cfrac{m.g.h}{t}$ (výsledný vzorec) 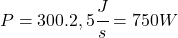$P=\cfrac{90 kg.10\frac{N}{kg}.2,5m}{3 s}$ $P=300.2,5 \cfrac{J}{s}=750 W$ Odpoveď:
Vzpierač podal priemerný výkon 750 watov.
Žeriav má motor s maximálnym výkonom 4,5 kilowatov, zdvíha náklad s hmotnosťou 1,5 tony do výšky 30 m. Aký je minimálny čas, za ktorý to dokáže vykonať?
Zápis:
P=4,5 kW=4500 W
m=1,5 t=1500 kg
h=30 m
t=?
Riešenie:
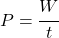$P=\cfrac{W}{t}$ (obe strany vynásobíme t a predelíme P)
$t=\cfrac{W}{P}$
$W=F.s=F.h$
$F=m.g$
$t=\cfrac{m.g.h}{P}=\cfrac{1500 kg.10\frac{N}{kg}.30m}{4500 W}$
$t=\cfrac{450000 N.m}{4500 W}=100 s$
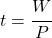
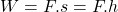
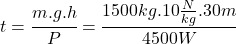
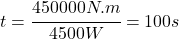
Odpoveď:
Minimálny čas, ktorý bude žeriav potrebovať na zdvihnutie nákladu, je 100 sekúnd.
Traktor pôsobí na pluh silou 10000 newtonov a pohybuje sa rovnomerne priamočiarym pohybom rýchlosťou 18 km za hodinu. Aký podáva pri orbe výkon?
Zápis:
$F=10000\,N$
$v=18 km/h$
$P=?$
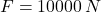
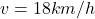
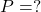
Riešenie:
$P=\cfrac{W}{t}$
$W=F.s$
$P=\cfrac{F.s}{t}=F.\cfrac{s}{t}=F.v$
$v=18\,\frac{km/h}=\cfrac{18000\,m}{3600\,s}=5\frac{m}{s}$
$P=10000\, N.5\,\frac{m}{s}=50000\, W=50\, kW$
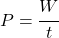
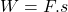
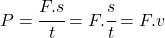
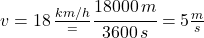
Odpoveď: Traktor pri orbe podáva výkon 50 kilowatov.
Potápači na dne mora v hĺbke 25 metrov objavili delovú hlaveň s hmotnosťou 300 kg. Hlaveň je z kovu s hustotou 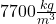$7700 \frac{kg}{m^3}$ . Hustota morskej vody je 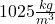$1025 \frac{kg}{m^3}$ , paluba lode je $1,5$ metra nad hladinou. Akú veľkú mechanickú prácu vykonajú, keď vyzdvihnú hlaveň na palubu.
Zápis:
$m=25\, m$
$h_1=25\, m$
$h_2=1,5\, m$
$\rho_1=7700\, \frac{kg}{m^3}$
$\rho_2=1025\, \frac{kg}{m^3}$
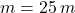
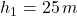
Rozbor: Pod hladinou mora pôsobí hydrostatická vztlaková sila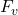 $F_v$ . Nad hladinou mora táto sila nepôsobí, preto musíme vypočítať vztlakovú silu a celková práca sa bude skladať z práce pod hladinou a z práce nad hladinou.
Riešenie:
$W=W_1+W_2$
$W_1=F_1.h_1\hspace{1cm}W_2=F_2.h_2$
$F_1=F_g-F_v\hspace{1cm}F_2=F_g$
$F_g=m.g$
$F_v=V.\rho_2.g$
$V=\cfrac{m}{\rho_1}$
$W=m.g.h_1-\cfrac{\rho_2}{\rho_1}.m.g._h1+m.g.h_2$
$W=m.g.(h_1+h_2)-\cfrac{m}{\rho_1}.\rho_2.g.h_1$
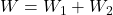
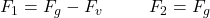
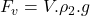
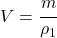
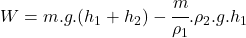
Príklad nad rámec toho, čo by ste mali vedieť.
Vráťme sa k príkladu so žeriavom. Pri riešení sme sa dopustili niekoľkých nepresností. Pohyb nákladu sa skladá z troch fáz. V prvej fáze sa náklad pohybuje zrýchlene, v druhej sa pohybuje rovnomerne priamočiarym pohybom a v poslednej fáze sa pohybuje spomaleným pohybom. V idealizovanom prípade predpokladajme, že celú dráhu sa náklad pohyboval rovnomerným priamočiarym pohybom. V príklade s traktom sme zistili, že výkon je priamo úmerný sile a rýchlosti: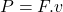 $P=F.v$
Maximálna rýchlosť, ktorou dokáže žeriav s takýmto nákladom vyvinúť j
$v=\cfrac{P}{F}=\cfrac{4500 W}{1500 kg.10 \frac{N}{kg}}$
$v=0,3\,m/s$
$t=\frac{s}{v}=\frac{30\,m}{0,3\, \frac{m}{s}}=100 s$
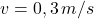
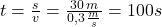
Znova nám vyšlo 100 sekúnd. Pri zadaní nebola uvedená hmotnosť háku na ktorom je teleso zavesené, tiež sme zanebali trenie. Skutočný čas bude teda o niekoľko sekúnd dlhší.

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Pridaj komentár Zrušiť odpoveď