Logické spojky (logické operácie)

Výroky môžeme spájať logickými spojkami. Spojením dvoch elementárnych výrokov vznikne zložený výrok. Logické spojky predstavujú operátory logických operácií.

negácia – pred pôvodný výrok napíšeme nie je pravda že, tiež môžeme napísať predponu ne-. Negáciu výroku A môžeme označiť A‘ alebo použiť operátor $\neg$ . Pri programovaní alebo v exceli používame NOT.
konjukcia – a, ako operátor sa namiesto a môžu použiť 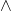$\wedge$ , &. Pri programovaní alebo v exceli AND
disjunkcia – alebo, ako operátor sa namiesto alebo používa 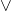$\vee$ . Pri programovaní a v exceli OR.
exkluzívna disjunkcia – vylučujúce alebo, buď … alebo. Ako operátor použijeme pri programovaní a exceli XOR, pri matematickom zápise môžeme použiť $\oplus$ .
implikácia – ak A potom B, ak A tak B, z A vyplýva B, A implikuje B. Ako operátor používame $A\implies B$
ekvivalencia – A práve vtedy a len vtedy ak B. Ako operátor používame $A\iff B$

Negácia

Negácia je unárna operácia (má len jeden operand). Operátorom negácie je nie je pravda že, alebo ne-, v matematickom zápise apostrof nad výrokom alebo $\ neg$ . Negácia je opačný výrok k pôvodnému výroku. Ak bol výrok pravdivý, jeho negácia je nepravdivá, ak bol nepravdivý, jeho negácia je pravdivá. Negáciou negácie je pôvodný výrok.

Bežný jazyk je v tomto smere vágny (nepresný, nejednoznačný). Keď povieme „Nie, neprší“, tak asi máme na mysli „Neprší“, hoci by to mohlo znamenať „Prší“, keďže sme prší dvakrát znegovali (popreli).

A=Prší. A‘=Neprší. A‘=Nie je pravda, že prší.

Pravdivostná tabuľka pre negáciu

A	A‘	(A‘)‘
0 1	1 0	0 1

Konjukcia

Konjukcia je binárna operácia (má dva operandy). Logickým operátorom konjukcie je a, v matematickom zápise $\wedge$ . Konjukciu nazývame aj logický súčin pretože jej pravdivostné hodnoty zodpovedajú binárnemu súčinu pravdivostných hodnôt oboch výrokov. Konjukcia je pravdivá, ak oba výroky sú pravdivé.

Pravdivostná tabuľka konjukcie

$A$	$B$	$A \wedge B$
0 0 1 1	0 1 0 1	0 0 0 1

Disjunkcia

Disjunkcia je binárna operácia. Jej operátorom je logická spojka alebo, v matematickom zápise $\vee$ . V bežnej reči obvykle ak použijeme slovo alebo, máme na mysli, že nastane práve jedna z možností. Alebo v logike predstavuje aj možnosť, že obe možnosti nastanú, čiže zložený výrok je nepravdivý, len ak sú oba výroky nepravdivé.

Pravdivostná tabuľka disjunkcie

A	B	A $\vee$ B
0 0 1 1	0 1 0 1	0 1 1 1

Vylučujúce alebo

Vylučujúce alebo (angl. exclusive or) je binárna logická operácia. Jej operátorm je logická spojka buď … alebo …, v matematickom zápise $\oplus$ , v exceli XOR. Zložený výrok je pravdivý, ak je pravdivý práve jeden z výrokov A, B.

A	B	A xor B
0 0 1 1	0 1 0 1	0 1 1 0

Implikácia

Implikácia je binárna logická operácia. Jej operátorom je logická spojka Ak … potom …, alebo Ak … tak …, v matematickom zápise $\implies$ . Platnosť výroku A je postačujúcou podmienkou pre platnosť výroku B, ale nie je nutnou podmienkou pre platnosť B. Napríklad výrok: Ak prirodzené číslo n končí číslicou 0, potom je deliteľné 5 je pravdivý. Ale ak číslo n končí 5, tiež je deliteľné 5.

Pravdivostná tabuľka implikácie

Ak máme postupnosť pravdivých implikácií $A\implies B, B \implies C, C\implies D$ potom je pravdivá aj implikácia $A \implies D$

Obrátená implikácia: K implikácii $A \implies B$ je obrátenou implikáciou $B \implies A$ . Hoci je pôvodná implikácia pravdivá, obrátená implikácia pravdivá byť nemusí. Výrok Ak je prirodzené číslo n deliteľné 5, potom číslo n končí číslicou 0 nie je pravdivý. Napríklad číslo 25 je deliteľné 5 a končí 5.

Ak je na oblohe dúha, potom prší. Výrok je pravdivý, bez dažďa dúha na oblohe byť nemôže.

Obrátená implikácia je: Ak prší, potom je na oblohe dúha. Výrok pravdivý nie je, väčšinou keď prší, dúha nevznikne. Musí navyše svietiť slnko a musíme stáť v istom rozpätí uhlov medzi dažďom a slnkom.

Skúsme výrok Ak je na oblohe dúha, potom prší, zmeniť tak aby vznikla implikácia, kde by si výroky vymenili miesta, trochu sme ich upravili a táto implikácia aby bola pravdivá. Ak neprší, nie je na oblohe dúha. Tento výrok je pravdivý a nazývame ho obmenená implikácia.

Obmenená implikácia k výroku $A \implies B$ je výrok $B'\implies A'$ .

Obmenená implikácia má rovnakú pravdivostnú hodnotu, ako pôvodná implikácia.

Pravdivostná tabuľka implikácie a obmenenej implikácie

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Pridaj komentár Zrušiť odpoveď

A	B	A‘	B‘	$A \implies B$	$B' \implies A'$
0 0 1 1	0 1 0 1	1 1 0 0	1 0 1 0	1 1 0 1	1 1 0 1