Lineárna rovnica

Lineárna rovnica je každá rovnica, ktorú môžeme „korektnými“ úpravami previesť na tvar: $a\cdot x+b=0$
kde $a,b \in R, \, a\neq 0$ .

„Korektné“ úpravy sú také úpravy, ktoré nezmenia riešenie rovnice. Úpravy ktoré nemenia riešenie rovnice nazývame ekvivalentné úpravy.

ekvivalentný – majúci rovnakú cenu, hodnotu, rovnocenná náhrada

Ekvivalentné úpravy

Rovnicu si môžeme predstaviť ako rovnoramenné váhy, ktoré sú v rovnováhe. Ak na obe strany váh pridáme rovnaké závažie, rovnováha sa nezmení. Ak z oboch strán zoberieme rovnaké závažie, rovnováha sa nezmení. Ak som mal na ľavej strane tri rovnaké objekty a závažia ž1 a ž2 na pravej strane, ak znásobím počet objektov vľavo dvoma a na pravej strane bude dvojnásobný počet závaží, rovnováha sa nezmení. Ak som mal vľavo tri rovnaké objekty a vpravo tri rovnaké závažia, ak budem mať vľavo jeden objekt a vpravo jedno závažie, rovnováha sa nezmení.

Pridaniu závaží zodpovedá pripočítanie rovnakého výrazu k obom stranám. Odobratiu závaží zodpovedá odpočítanie rovnakého výrazu od oboch strán. Znásobeniu objektov na jednej a druhej strane zodpovedá násobenie rovnakým výrazom. Predeleniu počtu objektov na jednej a druhej strane zodpovedá delenie rovnakým výrazom. Ak vymeníme strany na rovnoramenných váhach, rovnováha sa zachová.

Ekvivalentné úpravy teda sú:

pripočítanie rovnakého výrazu k obom stranám rovnice
odčítanie rovnakého výrazu od oboch strán rovnice
vynásobenie oboch strán rovnice rovnakým výrazom rôznym od nuly (ak by sme násobili nulou, tak to čo sa pôvodne nerovnalo by sa zrazu rovnalo, napr. $2\neq 1 /.0, 0=0)$
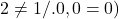
delenie oboch strán rovnice rovnakým výrazom rôznym od nuly (nulou sa nedá deliť)
výmena oboch strán rovnice

Ak rovnicu prevedieme do tvaru $a\cdot x+b=0$ jej riešením je $x=\dfrac{-b}{a}$

Hodnota x pre ktorú rovnosť platí nazývame riešenie rovnice alebo koreň rovnice.

Neznáma: x v rovnici nazývame neznáma.

Príklad 1 (bol aj vo videu) : 3x+4=x+6

$3x+4=x+6 / -x$
$3x-x+4=x-x+6$
$2x+4=6 / -4$
$2x+0=6-4$
$2x=2 / :2$
$2x:2=2:2$
$\underline {x=1}$

Skrátené riešenie (môžete medzikroky počítať naspamäť, ale častejšie sa pomýlite)

$3x+4=x+6 / --x-4$
$2x=2 / :2$
$\underline {x=1}$

Príklad 2:

$x+1=2(3,5-x)$ Najprv roznásobíme výraz v zátvorkách
$x+1=7-2x\, / +2x$ Za lomenou čiarou napíšeme operáciu, ktorú vykonáme na oboch stranách rovnice
$3x+1=7 \, / -1$
$3x=6\, / :3$
$x=2$

Keď rovnicu vyriešime, urobíme skúšku správnosti. Koreň rovnice dosadíme do výrazu na ľavej strane a potom do výrazu na pravej strane. Ak ich hodnoty budú rovnaké, skúška správnosti nám vyšla, rovnicu sme vyriešili správne.

$L: 2+1=3$
$P: 2(3,5-2)=2\cdot 1,5=3$
$L=P$

Riešením rovnice je $x=2$ .

Príklad:

$\dfrac{x-1}{x+1}=2 / \cdot (x+1), x+1\neq 0, x\neq -1$
$x-1=2x+2 / -x-2$
$-3=x$
$x=-3$

Skúška správnosti:

$L: \dfrac{-3-1}{-3+1}=\dfrac{-4}{-2}=2$
$L=P$

Riešením rovnice je $x=-3$ .

Príklad:

$\dfrac{x+1}{x+1}=2 / \cdot (x+1), x\neq -1$
$x+1=2x+2 /-x-2$
$-1=x\, teda\, x=-1$

Podmienka v prvom riadku bola $x\neq -1$ , takže -1 nie je riešením rovnice. Môžeme sa presvedčiť dosadením do rovnice, dostaneme $\dfrac{0}{0}$ a nulou deliť nevieme. Táto rovnica nemá riešenie. V podstate sme na to mohli prísť hneď na začiatku, pretože sme mali rovnaký výraz v čitateľovi aj v menovateľovi a delenie čísla rovnakým číslom je vždy 1 okrem 0/0. Na tomto príklade vidno, aké dôležité sú podmienky alebo skúška správnosti.

Príklad:

$\dfrac{x+1}{x+1}=1 /\cdot (x+1) x\neq -1$
$x+1=x+1 / -x-1$
$0=0$

Vyšlo nám 0=0, to je pravda, ale čo je riešením rovnice? Riešením rovnice sú všetky reálne čísla okrem -1. Delíme rovnaký výraz rovnakým výrazom, takže ak dosadíme konkrétne číslo za x, delíme rovnakú hodnotu rovnakou hodnotou a to je vždy jedna, okrem delenia nulou.

Slovné úlohy, ktoré možno riešiť zostavením lineárnej rovnice

Trieda sa zúčastnila zubnej prehliadky. Štvrtine žiakov triedy zistili jeden zubný kaz, osmine dva zubné kazy a polovica triedy nemala zubné kazy. Koľko žiakov má trieda, ak 4 žiaci chýbali?
Cez prázdniny bolo 159 žiakov ubytovaných v troch chatách. V chate B bolo o osem žiakov viac než v chate B a v chate C o 14 viac než v chate B. Koľko žiakov bolo ubytovaných v jednotlivých chatách?
Za tri dni prešli žiaci na výlete 65 km. Prvý deň prešli dvakrát toľko ako tretí deň, druhý deň prešli o 10 km menej ako prvý deň. Koľko km prešli v jednotlivé dni?

Riešenia

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Pridaj komentár Zrušiť odpoveď