Štatistické charakteristiky

Štatistické charakteristiky sú hodnoty, ktoré charakterizujú štatistický súbor ako celok. Medzi štatistické charakteristiky patria:

aritmetický priemer
geometrický priemer
kvadratický priemer
harmonický priemer
medián
modus
smerodajná odchýlka
rozptyl
korelácia

Aritmetický priemer

Aritmetický priemer alebo iba priemer štatistického znaku štatistického súboru vypočítame tak, že spočítame všetky hodnoty štatistického znaku a predelíme ju rozsahom štatistického súboru:

$\overline{x}=\dfrac{\displaystyle{\sum_{i=1}^n} x_i}{n}$

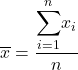
alebo

$\overline{x}=\dfrac{x_1+x_2+...+x_n}{n}$

Vážený aritmetický priemer vypočítame tak, že spočítame početnosti jednotlivých hodnôt štatistických znakov, tieto početnosti vynásobíme hodnotami znakov, výsledky sčítame a výslednú sumu predelíme rozsahom štatistického súboru. Nech štatistický znak nadobúda k hodnôt:

$\overline{x}=\dfrac{\displaystyle{\sum_{i=1}^k} n_i\cdot x_i }{n}$

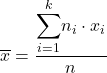
alebo

$\overline{x}=\dfrac{n_1\cdot x_1+ n_2\cdot x_2+...+ n_k\cdot x_k}{n}$

Aritmetický priemer a vážený aritmetický priemer majú rovnakú hodnotu, sú to len iné matematické metódy na výpočet priemernej hodnoty. Výpočet váženého aritmetického priemeru je rýchlejší, ak sú absolútne početnosti väčšie. Napríklad 400 žiakov školy ma priemerne 20 známok. Aritmetický priemer by sme vypočítali 7999 operáciami sčítania. Vážený priemer by sme vypočítali 5 operáciami násobenia a 4 operáciami sčítania (známky nadobúdajú iba 5 hodnôt).

Poznámka: Znak $\sum$ čítame ako suma. Predstavuje súčet výrazov, kde index ide od nejakej prvotnej hodnoty uvedenej pod znakom po hodnotu uvedenú nad znakom $\sum$ .

Príklad 1: Žiaci sa navzájom odmerali a na tabuľu zapísali nasledujúce hodnoty svojich výšok: Tibor 178, Peter 184 Karol 164 Petra 170 Ivana 165 Eva 158 Ivan 175 Adam 175 Dušan 170 Dana 164
Vypočítajte:
a) aritmetický priemer výšky žiakov
b) vážený priemer výšky žiakov
c) aritmetický priemer výšky chlapcov
d) aritmetický priemer výšky dievčat

Riešenie: žiakov je $n=10$ , chlapcov je $n_c=6$ , dievčat je $n_d=4$

Súčet všetkých výšok je:

$s=178+184+164+170+165+158+175+175+170+164=1703$

Aritmetický priemer: $\overline{v}=\dfrac{s}{n}= \dfrac{1703\, cm}{10} =170,3\, cm$

Vážený priemer: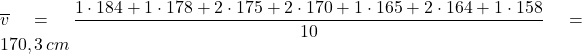
$\overline{v} = \dfrac{1\cdot 184+ 1\cdot 178+2 \cdot 175+2 \cdot 170+ 1\cdot 165+ 2\cdot 164+1 \cdot 158 }{10} =170,3\, cm$

Priemerná výška chlapcov: $\overline{v}_c=\dfrac{178+184+164+175+175+170}{6}=\dfrac{1046}{6}\doteq 174,33$

Priemerná výška dievčat:

$\overline{v}_c=\dfrac{170+165+158+164}{4}=\dfrac{657}{4}= 164,25$

Geometrický priemer sa počíta podľa vzorca:

$\overline{x}_g=\sqrt[n]{x_1\cdot x_2\cdot ...\cdot x_n}$

Geometrický priemer je menší alebo rovný aritmetickému priemeru. Arimetickému priemeru je rovný, len ak sú všetky hodnoty rovnaké.

Geometrický priemer sa používa napríklad pri určení priemerného rastu ekonomiky alebo priemerného výnosu. Napríklad: ak by rast cien bol 20%, 10%, -15%, 10%, koeficienty rastu by boli 1,2 1,1 0,85 a 1,1. Geometrický priemer koeficientov rastu by bol:
$\overline{k}_g=\sqrt[4]{1,2\cdot 1,1\cdot 0,85\cdot 1,1}\doteq1,054$

Ak by ceny celý čas rástli tempom o 5,4%, výsledný rast cien by bol rovnaký.

Žiaci by mali po učiteľoch požadovať, aby im známky na vysvedčení počítali geometrickým priemerom. Napríklad pre 5 a 1 je aritmetický priemer 3 a geometrický priemer je: $\sqrt{5\cdot 1}\doteq2.24$

Ostatné druhy priemerov sa vo vašej praxi pravdepodobne nevyskytnú a preto ich nebudeme preberať. Ak by vás zaujímali, pozrite si literatúru uvedenú v zdrojoch.

Napríklad stredná kvadratická rýchlosť molekúl plynu sa používa v štatistickej fyzike pri skúmaní plynov.

Medián

Medián je hodnota, ktorá usporiadaný zoznam hodnôt štatistického znaku rozdelí na dve rovnaké časti. V štatistickom súbore sa vyskytlo rovnako veľa menších alebo rovnakých a rovnako veľa väčších alebo rovnakých hodnôt. Ak je rozsah súboru nepárny, medián možno určiť jednoznačne, ak je párny, mohli by sme vybrať ľubovoľnú hodnotu medzi hodnotami na mieste $\frac{n}{2}\, a\, \frac{n}{2}+1$ . Obvykle zvolíme ich aritmetický priemer.

Medián niekedy lepšie vystihuje rozloženie hodnôt v štatistickom súbore než aritmetický priemer. Napríklad priemerný mesačný príjem vo firme kde má 8 robotníkov 500 euro, vedúci 1000 euro a majiteľ firmy 5000 euro by bol $\overline{m}=\dfrac{8\cdot 500+1000+5000}{10}=1000$ euro. Medián by bol 500 euro.

Medián možno definovať aj na kvalitatívne štatistické znaky, ktoré možno zmysluplne usporiadať napr. najvyššie dosiahnuté vzdelanie.

Medián patrí medzi kvantily. Kvantily rozdeľujú usporiadaný štatistický súbor na rovnako veľké časti. Decil je desatina súboru, percentil je stotina súboru. S percentilom ste sa stretli na monitore v 9. ročníku ZŠ, ak ste dosiahli percentil 50, 50 percent žiakov dosiahlo horší výsledok ako vy.

Modus

Modus je najčastejšia hodnota štatistického znaku. Modusov môže byť viac.

Modus na rozdiel od priemeru možno uplatniť aj na kvalitatívne znaky. Ak je v triede 7 dievčat a 12 chlapcov, modus je chlapec. Ak by ich bolo 7 a 7 modus by bol aj chlapec aj dievča.

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Aritmetický priemer

One Comment

Pridaj komentár Zrušiť odpoveď