Počas hodiny sme vykonali nasledujúce pokusy:
Prvý pokus
Na laboratórnom stole som ku koncu naklonenej roviny priložil vrchnák z papierovej škatule. Z naklonenej roviny som postupne spúšťal tri oceľové guličky, každá mala iný polomer a teda inú hmotnosť. Na konci naklonenej roviny gulička narazila do nádobky a nádobka sa posunula.
- Meraním sme zistili, že posun nádobky bol priamo úmerný hmotnosti guličiek.
- Odmerail sme výšku, z ktorej sme guličky spúšťali a zväčšil sklon naklonenej roviny, výšku sme zväčšili na dvojnásobok.
- Očakávali sme, že nádobka sa pohne pri každej guličke o dvojnásobok. Nebolo tomu vždy tak, pretože časť energie guličiek sa spotrebovala pri náraze guličky o stôl (je logické, že sa to nechovalo podľa pôvodného očakávania, ak by sme sklon zväčšili na 90 stupňov, tak gulička by nádobkou nepohla vôbec). Navrhujem pokus zopakovať tak, že nezmeníme sklon, ale guličku spustíme z polovice dosky, bude sa gúľať z polovičnej výšky.
Z pokusu sme usúdili:
- Pohybujúce sa teleso je schopné konať prácu.
- Guličky som spúšťal z rovnakej výšky, na konci dráhy mali (ak zanedbáme trenie a to, že guličky sa správajú aj ako zotrvačníky) rovnakú rýchlosť. Veľkosť práce, ktorú gulička bola schopná vykonať závisela priamo úmerne od jej hmotnosti a nejako závisela aj od jej rýchlosti,. Rýchlosť guličiek sme nemerali, takže konkrétnu závislosť sme nezistili.
Druhý pokus:
Stlačil som oceľovú pružinu, priložil ju k oceľvej guličke a keď som pružinu pustil, narazila do guličky a guličku vystrelila.
Z pokusu sme usúdili, že stlačená alebo natiahnutá pružina je schopná konať prácu.
Tretí pokus:
Na koncoch tyčových magnetov boli oceľové guličky, dva tyčové magnety som priložil k sebe tak, že sa guličky dotýkali a rovnaké póly magnetov boli pri sebe. Keď som jeden z magnetov pustil, tento magnet sa začal kotúľať preč.
Z pokusu môžeme usúdiť, ak vykonáme prácu, ktorou priblížime magnety k sebe, pričom sú orientované tak, že sa odpudzujú, vykonaná práca sa nestratí, ale po odstránení vonkajšej sily, sa premení na pohybovú energiu jedného alebo oboch magnetov.
Tretí pokus sme modifikovali tak, že sme sa k jednému z magnetov približovali druhým magnetom nesúhlasnými pólmi. V istej vzdialenosti príťažlivá sila magnetov prekonala valivé trenie a magnety sa začali k sebe kotúľať rýchlejšie a rýchlejšie, až do seba narazili.
Štvrtý pokus
Medzi dva magnety z predchádzajúceho pokusu som položil tretí, znova tak, že rovnaké póly boli pri sebe. Keď som sa niektorým z krajných magnetov priblížil k magnetu v strede, tento sa rozkotúľal k druhému, od neho sa začal kotúľať späť a takto medzi nimi periodicky kmital. Keďže išlo o valivé trenie, straty energie boli malé a magnet kmital pomerne dlho.
Schopnosť konať prácu nazývame energia, značka ![]() .
.
V mechanike rozoznávame dva druhy energie:
- pohybová energia (kinetická energia) – je energia pohybujúceho sa telesa. Budeme ju označovať

- polohohová energia (potenciálna energia) – je energia, ktorú teleso má kvôli svojej polohe. Budeme ju označovať
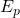
Oba druhy energie nazývame súhrnným názvom mechanická energia. Keďže existujú aj iné druhy enegie, než je mechanická, budeme ju označovať ![]() .
.
Poznámky:
- Ak bude z kontextu jasné, že ide o mechanickú energiu, môžeme index mech vynechať.
- V článkoch budem dávať prednosť termínu kinetická energia pred pohybová energia.
V troch vyššie uvedených pokusoch sme mali tri rôzne príčiny (zdroje) polohovej energie:
- v prvom pokuse bolo príčinou polohovej energie gravitačné pole Zeme
- v druhom bola príčinou pružná deformácia oceľovej pružiny
- v treťom bolo príčinou magnetické pole magnetov
Preskúmajme podrobnejšie vzťah medzi polohovou energiou telesa v gravitačnom poli a kinetickou energiou. Keď zmena výšky nie je veľká, môžeme gravitačné pole Zeme pokladať za homogénne, gravitačná sila je vo všetkých polohách rovnaká (konštantná).
Keď zdvihneme teleso s hmotnosťou ![]() do výšky
do výšky ![]() , vykonáme prácu (1)
, vykonáme prácu (1)
![]()
Ak ho z tejto výšky pustíme na zem, začne padať rovnomerne zrýchleným pohybom a dopadne rýchlosťou ![]() . Vypočítajme, akou rýchlosťou dopadne. Pre rovnomerne zrýchlený pohyb platí (2)
. Vypočítajme, akou rýchlosťou dopadne. Pre rovnomerne zrýchlený pohyb platí (2)
![]()
pre dráhu rovnomerne zrýchleného pohybu sme odvodili (3)
![]()
V našom prípade je ![]() rovné
rovné ![]() , a
, a ![]() je rovné
je rovné ![]() . Dosadením do (3) dostaneme:
. Dosadením do (3) dostaneme:
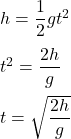
Dosadením pravej strany do (2) namiesto ![]() dostaneme (4)
dostaneme (4)
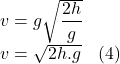
Celková mechanická energia telesa je súčtom pohybovej a polohovej energie.
![]()
Z bežných životných skúseností vieme, že ak pustíme loptičku z výšky ![]() , čím je loptička pružnejšia a podložka tvrdšia, loptička po odraze vyskočí do väčšej výšky. Táto výška odrazu
, čím je loptička pružnejšia a podložka tvrdšia, loptička po odraze vyskočí do väčšej výšky. Táto výška odrazu ![]() býva menšia než
býva menšia než ![]() . Do pôvodnej výšky by loptička vyskočila, ak by bola dokonale pružná, podložka dokonale pevná a vzduch by nespôsoboval odpor.
. Do pôvodnej výšky by loptička vyskočila, ak by bola dokonale pružná, podložka dokonale pevná a vzduch by nespôsoboval odpor.
Na vzťah (4) sa môžeme pozrieť aj z opačného konca. Do akej výšky ![]() vyletí teleso, ak ho vyhodíme počiatočnou rýchlosťou
vyletí teleso, ak ho vyhodíme počiatočnou rýchlosťou ![]() ? Dostaneme
? Dostaneme
![]()
Pokiaľ by počas letu telesa nepôsobil odpor vzduchu, platilo by, že súčet polohovej a pohybovej energie je konštantný. Pri výstrele je polohová energia nulová a pohybová je maximálna, na vrchole dráhy je rýchlosť telesa nulová a polohová je maximálna. Potom jedna i druhá maximálna energia sú rovnaké:
![]()
Keď sme teleso vystrelili, malo rýchlosť ![]() , bolo vo výške 0. Jeho kinetická energia bola rovnaká, akú malo polohovú energiu, keď dosiahlo maximálnu výšku. Ak za
, bolo vo výške 0. Jeho kinetická energia bola rovnaká, akú malo polohovú energiu, keď dosiahlo maximálnu výšku. Ak za ![]() dosadíme pravú stranu z rovnice (4.1) dostaneme
dosadíme pravú stranu z rovnice (4.1) dostaneme
![]()
Pre kinetickú energiu teda platí (6)
![]()
a pre celkovú mechanickú energiu dostaneme (7)
![]()
Zo vzťahu (6) vyplýva, že kinetická energia je priamo úmerná druhej mocnine rýchlosti. Teda, ak rýchlosť zdvojnásobime, kinetická energia vzrastie na dvojnásobok.
Praktické dôsledky: Ak ideme v aute dvojnásobne veľkou rýchlosťou a zbadáme prekážku, brzdná dráha vozidla bude 4 krát dlhšia, pretože sa musí vynaložiť 4 krát väčšia práca na brzdenie, pričom sila ktorou sme schopní brzdiť je nanajvýš rovná maximálnemu pokojovému treniu. Ak brzdíme šmykom, tak sa brzdná dráha ešte predĺži.
Podrobnejšie v článku Bezpečnosť dopravy z hľadiska rýchlosti auta.
Zákon zachovania mechanickej energie: V izolovanej sústave, v ktorej neexistuje trenie a k dispozícii je len mechanická energia je súčet kinetickej a potenciálnej energie konštantný.
![]()
Terminologický slovník
Izolovaná sústava je súbor telies v ohraničenom priestore, ktoré pôsobia iba medzi sebou a nepôsobia na ne vplyvy, ktoré sú mimo túto sústavu. Reálne žiadna izolovaná sústava neexistuje, je to abstraktný pojem, pomocou ktorého môžeme zjednodušiť skúmanie fyzikálnych dejov. Ak môžeme vplyvy, ktoré sú mimo skúmanú sústavu zanedbať, môžeme reálnu sústavu vyhlásiť za izolovanú sústavu.
Poznámka: Červene a zelene sú označené vzťahy a pojmy, ktoré sú kľučové pri riešení príkladov na mechanickú energiu a pri popise dejov súvisiacich s mechanickou energiou..