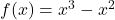Funkcia na množine D je ľubovoľný predpis, ktorý každému prvku množiny D priradí práve jedno reálne číslo. Funkciu označujeme malým písmenom.
Prvky množiny D nazývame nezávislá premenná, ich obrazy sú závislá premenná. Nezávislú premennú obvykle označujeme x a závislú y, ale môžeme zvoliť také označenie, aby bolo zrejmé čo tieto premenné označujú. napríklad ![]() , kde
, kde ![]() je dráha,
je dráha, ![]() je konštantná alebo priemerná rýchlosť a
je konštantná alebo priemerná rýchlosť a ![]() je čas.
je čas.
Definičný obor: Množinu D na ktorej je definovaná funkcia f(x) nazývame definičný obor funkcie. Značíme D(f(x)) alebo len D(f).
Obor hodnôt je množina hodnôt, ktoré funkcia môže nadobudnúť. Značíme H(f(x)) alebo len H(f).
Prostá funkcia je funkcia pre ktorú platí ![]()
Rastúca funkcia je funkcia pre ktorú platí ![]()
Klesajúca funkcia je funkcia pre ktorú platí ![]()
Neklesajúca funkcia je funkcia, pre ktorú platí: ![]()
Nerastúca funkcia je funkcia, pre ktorú platí: ![]()
Konštantná funkcia je funkcia, pre ktorú platí ![]()
Monotónna funkcia je funkcia, ktoré je rastúca alebo klesajúca alebo neklesajúca alebo nerastúca alebo konštantná.
Maximum funkcie je najväčšia hodnota, ktorú funkcia nadobudne. ![]()
Minimum funkcie je najmenšia hodnota, ktorú funkcia nadobudne. ![]()
Extrém funkcie je maximum alebo minimum.
Paradox: Konštantná funkcia má maximum aj minimum a maximum je rovné minimu.
Lokálne maximum a lokálne minimum: Ak na otvorenom intervale existuje maximálna alebo minimálna hodnota funkcie v rámci tohto intervalu, nazveme ju lokálne maximum alebo lokálne minimum.
Napríklad funkcia ![]() nemá maximum a nemá minimum, ale má lokálne maximum v bode 0 a lokálne minimum v bode 2/3. Graf:
nemá maximum a nemá minimum, ale má lokálne maximum v bode 0 a lokálne minimum v bode 2/3. Graf: