Hydrostatický tlak

2.12.2016MatematikaTibor Menyhért

Zo skúsenosti vieme, že s rastúcou hĺbkou rastie tlak vody. Od čoho závisí veľkosť tohto tlaku?

Pre tlak platí vzorec: $p=\cfrac{F}{S}$

Na vodu pôsobí gravitačná sila. Stĺpec vody v hĺbke $h$ pôsobí silou, ktorá je rovná gravitačnej sile. $F_g=m.g$ , kde $m$ je hmotnosť stĺpca vody.

Ak si vodu, ktorá pôsobí v hĺbke $h$ , predstavíme, ako fiktívny kváder so stranami $a\, ,b\,,h$ (namiesto $c$ tu máme $h$ ), pre objem tohto kvádra platí $V=a.b.h$ , hmotnosť kvádra je $m=V.\rho$ , gravitačná sila pôsobiaca na kváder vody je $F_g=V.\rho.g=a.b.h.\rho.g$

Plocha, na ktorú táto sila pôsobí, je $S=a.b$ , tlak v hĺbke $h$ je potom:

$p=\cfrac{a.b.h.\rho.g}{a.b}$

$p=\rho.g.h$

Na hladinu vody pôsobí atmosferický tlak (označme ho $p_0$ ), potom výsledný tlak v hĺbke $h$ bude: $p=p_0+\rho.g.h$

Príklad:

Nech je pri jazere normálny tlak ( $p_n=1013,25 hPa$ ). V akej hĺbke bude na potápača pôsobiť dvojnásobne väčší tlak, než keď bol v člne?

Zápis:

$p_n=1013,25 hPa=101 325 Pa$

$g=10 \frac{N}{kg}$

$\rho=1000 \cfrac{kg}{m^3}$

$h=?$

Riešenie:

$p=2.p_n$

$p=p_n+\rho.g.h$

$2.p_n=p_n+\rho.g.h$

$h=\cfrac{p_n}{\rho.g}$

$h=\cfrac{101325 Pa}{1000 \cfrac{kg}{m^3}.10 \cfrac{N}{kg}}$

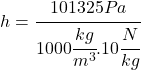
Pre pascal platí $1\, Pa=\cfrac{1N}{m^2}$ . Hore uvedený výraz možno previesť na nasledujúci tvar:

$h=\cfrac{102325\, \cfrac{N}{m^2}}{10000 \cfrac{N}{m^3}}$

$h=10,2325 m\approx 10,23 m$

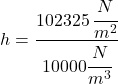
Odpoveď:

Na potápača bude pôsobiť dvojnásobný tlak oproti tlaku keď bol v člne v hĺbke 10,23 m.

Príklad 2: Ak by to nebolo sladkovodné jazero ale more, ako sa zmení výsledok?

Priemerná hustota morskej vody je $1025 kg/m^3$ .

Riešenie: Stačí dosadiť do výsledného vzorca namiesto $1000\, kg/m^3$ hodnotu $1025\, kg/m^3$ . Dostaneme $h=9,98\,m$ .

Odpoveď: V mori bude dvojnásobný tlak v hĺbke 9,98 m.

Z vyššie uvedeného môžeme povedať, že približne každých 10 m stúpne tlak o rovnakú hodnotu, ako je normálny atmosferický tlak.

print

2 Comments

Spätné upozornenie: Vztlaková sila. Archimedov zákon | Podklady pre výuku fyziky, informatiky a techniky
Spätné upozornenie: Články z fyziky 8. ročník – Stránka 8. A. Základná škola Krosnianska 4, Košice

Pridaj komentár Zrušiť odpoveď