Operácie s mnohočlenmi

Z mnohočlenmi môžeme robiť rovnaké operácie ako s číslami. Majme dva mnohočleny: $A(x)\, a\, B(x)$

sčítanie: $A(x)+B(x)$
odčítanie: $A(x)-B(x)$
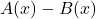
násobenie: $A(x)\cdot B(x)$
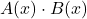
delenie: $A(x) : B(x)$

Sčítanie a odčítanie mnohočlenov je jednoduché, sčítame (odčítame) koeficienty jednotlivých stupňov, ak v niektorom mnohočlene nebol člen s daným stupňom implicitne tam je s koeficientom nula.

Napríklad: $A(x)=3x^3-2x^2+x+7,\, B(x)=4x^4-3x^3+x+3$

$A(x)+B(x)=4x^4-2x^2+2x+10$

$A(x)-B(x)=-4x^4+6x^3+4$

Násobenie je o čosi zložitejšie, každým členom prvého mnohočlena násobíme každý člen druhého mnohočlena.

Napríklad: $A(x)=2x+1,\, B(x)=6x^2-x-2$

$A(x)\cdot B(x)=(2x+1)\cdot (6x^2-x-2)=$

$2x\cdot 6x^2+2x\cdot (-x)+2x\cdot (-2)+ 6x^2-x- 2=12x^3+4x^2-5x-2$

Ak by sme násobili tri alebo viac mnohočlenov, najprv vynásobíme prvé dva, výsledkom vynásobíme tretí, poprípade novým výsledkom vynásobíme štvrtý, … Možeme poprípade využiť komutatívny zákon a činitele poprehadzovať tak, aby sa nám jednoduchšie počítalo.

Napríklad: $(x+1)(2x+2)(x-1)$ Najprv vynásobíme prvý a tretí činiteľ a výsledkom vynásobíme druhý, lebo $(x+1)(x-1)=x^2-1$

$(2x+2)(x^2-1)=2x^3-2x+2x^2-2=2x^3+2x^2-2x-2$

Poznámka: Je dobrým zvykom usporiadať mnohočlen podľa stupňov jeho členov.

Sčítaním, odčítaním a násobením mnohočlenov vzniká znova mnohočlen.

Delenie mnohočlenov je komplikovanejšie a výsledkom môže, ale nemusí byť mnohočlen. Budeme sa tomu venovať v inom článku.

Mocniny mnohočlena

Mocnina je násobenie toho istého čísla tým istým číslom, mocnina mnohočlena je násobenie toho istého mnohočlena tým istým mnohočlenom. Je dobré si zapamätať nasledujúce vzorce:

$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

Prvé dva sa dajú zapamätať ľahko, pri treťom a štvrtom si všimnite, že exponenty pri a klesajú od 3 po nulu a pri b stúpajú od nuly po 3. Vo štvrtom vzorci sa znamienka striedajú.

Súčin (a+b).(a-b)

$(a+b)\cdot (a-b)=a^2-a\cdot b+b\cdot a-b^2=a^2-b^2$

Aj tento vzťah je dobré si zapamätať, často ho možno použiť pri zjednodušovaní výrazov: $(a+b)\cdot (a-b)=a^2-b^2$

Podklady pre výuku matematiky, fyziky a informatiky

Nie je hanba nevedieť. Hanba je tváriť sa, že viem, hoci neviem.

Pridaj komentár Zrušiť odpoveď