Mnohočlen alebo polynóm n-tého stupňa je algebraický výraz v tvare:
![]()
kde ![]() sú číselné konštanty a
sú číselné konštanty a ![]() je premenná. Exponenty pri premennej sú prirodzené čísla, konštanty sú reálne čísla a
je premenná. Exponenty pri premennej sú prirodzené čísla, konštanty sú reálne čísla a ![]() .
.
Poznámka: termín polynóm pochádza z gréčtiny, kde poly je mnoho a nóm je člen.
Polynóm je napríklad: ![]() alebo
alebo ![]()
Polynóm môže obsahovať aj viacero premenným napríklad:
![]()
V polynóme ![]() môžeme jednotlivým členom priradiť tieto názvy:
môžeme jednotlivým členom priradiť tieto názvy:
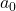 – absolútny člen
– absolútny člen  – lineárny člen
– lineárny člen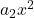 – kvadratický člen
– kvadratický člen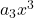 – kubický člen
– kubický člen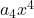 – člen štvrtého stupňa
– člen štvrtého stupňa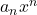 – člen n-tého stupňa
– člen n-tého stupňa
Opačný mnohočlen k mnohočlenu je taký mnohočlen, ktorý má opačné koeficienty v jednotlivých členoch. K mnohočlenu ![]() je opačný mnohočlen
je opačný mnohočlen ![]()
Príklad 1: Upravte daný výraz, určte stupeň mnohočlena a jeho koeficienty:
![]()
![]()
Mnohočlen je štvrtého stupňa a jeho koeficienty sú:
![]()
Všimnite si, že som uviedol aj koeficient ![]() , ktorý síce v mnohočlene nebol uvedený, ale implicitne tam bol, lebo
, ktorý síce v mnohočlene nebol uvedený, ale implicitne tam bol, lebo ![]() .
.
Príklad 2: Určite stupeň mnohočlena a absolútny člen z výrazu:
![]()
Napohľad vyzerá úloha zložito, ak by sme mali upraviť výraz na mnohočlen násobili by sme tri členy dvoma členmi a potom 6 členov 3 členmi. Spolu 24 operácií. Našou úlohou je ale určiť stupeň mnohočlena a absolútny člen. Stupeň mnohočlena určíme násobením mocnín najväčších stupňov v jednotlivých činiteľoch a absolútny člen násobením absolútnych členov činiteľov, dostaneme: ![]()
a ![]()
Odpoveď: Mnohočlen je 9 stupňa a jeho absolútny člen je -42.
Pri násobení mnohočlenov využívame komutatívny a distributívny zákon:

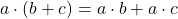 alebo
alebo 
Koreň polynómu je číslo ![]() , pre ktoré platí
, pre ktoré platí ![]() (namiesto x dosadíme koreň a hodnota polynómu vyjde rovná nule).
(namiesto x dosadíme koreň a hodnota polynómu vyjde rovná nule).
Príklad 3: Určte koreň polynómu x+3.
Riešenie: riešime lineárnu rovnicu ![]()
![]()
Príklad 4: Určte koreň polynómu ![]()
Riešenie a): ![]() Súčin je rovný nule, ak jeden z činiteľov je rovný nule. Potom má polynóm dva korene:
Súčin je rovný nule, ak jeden z činiteľov je rovný nule. Potom má polynóm dva korene: ![]()
Riešenie b): K obom stranám pripočítame ![]() . Dostaneme
. Dostaneme ![]()
![]()
Polynóm, ktorý má všetky koeficienty nulové nazývame nulový polynóm.
![]() . Takýto polynóm nemá žiaden stupeň.
. Takýto polynóm nemá žiaden stupeň.
Polynóm nultého stupňa je polynóm, ktorý má len absolútny člen, ktorý je nenulový.
Zdroje: