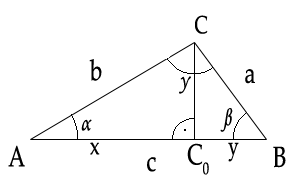
Majme trojuholník ABC, z vrcholu C veďme výšku na stranu c, ako ilustruje obrázok vpravo. Výška ![]() rozdelila trojuholník na dva pravouhlé trojuholníky
rozdelila trojuholník na dva pravouhlé trojuholníky ![]() a
a ![]() .
.
Pre oba trojuholníky platí Pytagorova veta:
![]()
![]()
![]()
![]()
![]()
![]()
Strana ![]() je spoločná strana trojuholníkov a vyjadrili sme ju v tvare
je spoločná strana trojuholníkov a vyjadrili sme ju v tvare ![]() a
a ![]() , potom platí:
, potom platí:
![]()
![]()
![]()
![]()
Tak isto by sme podobný vzťah dokázali pre strany b a c.
Kosínusová veta
![]()
![]()
![]()
Všimnite si posledný vzorec! Ak by ![]() bol pravý uhol, kosínus gama by bol rovný nule a kosínusová veta sa zmení na Pytagorovu vetu. Pytagorova veta je špeciálny prípad kosínusovej vety.
bol pravý uhol, kosínus gama by bol rovný nule a kosínusová veta sa zmení na Pytagorovu vetu. Pytagorova veta je špeciálny prípad kosínusovej vety.
Príklad:
Trojuholník ![]() má strany a=8 cm, b=7 cm a c=11 cm. Aké veľké sú uhly
má strany a=8 cm, b=7 cm a c=11 cm. Aké veľké sú uhly ![]() ?
?
Pri riešení využijeme kosínusovú vetu.
![]()
![]()
Zdroje:
- Obrázok a časť textu sú prevzaté a upravené z wikipédie