Mocninová funkcia je funkcia v tvare: ![]()
Preskúmajme vlastnosti mocninovej funkcie, ak je n celé číslo. Celé čísla môžu byť kladné alebo záporné, párne alebo nepárne. Nech n je párne kladné číslo Preskúmajme vlastnosti funkciíDo tabuľky vypíšme hodnoty týchto funkcií pre čísla -3;-2;-1;-0 a pre k nim opačné čísla:
|-3|-2|-1| -0,5|0| 0,5 | 1| 2| 3 _________________________________________
| 9| 4| 1| 0,25|0| 0,25| 1| 4| 9 _________________________________________
|-9|-4|-1|-0,25|0|-0,25|-1|-4|-9
Grafy týchto funkcii sú na tomto obrázku (graf bol zostrojený pomocou vyhľadávača google, ako vyhľadávaný výraz som zadal x^2,-x^2, prvá funcia je modrá, druhá je červená):

Vlastnosti funkcie ![]() :
:
Definičný obor: ![]()
Obor hodnôt: ![]()
Extrémy: má minimum v bode ![]() a
a ![]() , nemá maximum.
, nemá maximum.
Kde rastie a kde klesá: na intervale ![]() klesá na intervale
klesá na intervale ![]() rastie. V bode
rastie. V bode ![]() ani nerastie ani neklesá.
ani nerastie ani neklesá.
Prostosť funcie: funkcia nie je prostá, napríklad ![]()
Vlastnosti funcie ![]() :
:
Definičný obor: ![]()
Obor hodnôt: ![]()
Extrémy: má maximum v bode ![]() a
a ![]() , nemá minimum.
, nemá minimum.
Kde rastie a kde klesá: na intervale ![]() rastie na intervale
rastie na intervale ![]() klesá. V bode
klesá. V bode ![]() ani nerastie ani neklesá.
ani nerastie ani neklesá.
Prostosť funcie: funkcia nie je prostá, napríklad ![]()
Rovnaké vlastnosti by mali aj ostatné funcie s párnym kladným mocniteľom, iba by prudšie rástli a klesali.
Nech n je kladné a nepárne
Preskúmajme funkcie ![]()
V tabuľke sú hodnoty funcií pre rovnaké čísla, ako v predchádzajúcom prípade:
| -3|-2|-1| -0,5|0| 0,5 | 1| 2| 3
_________________________________________
|-27|-8|-1|-0,125|0| 0,125| 1| 8|27
_________________________________________| 27| 8| 1| 0,125|0|-0,125|-1|-8|-27
Grafy týchto funkcií sú na tomto obrázku, prvá je nakreslená modrou, druhá červenou farbou.
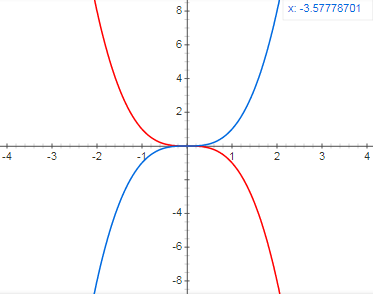
Vlastnosti funkcie ![]() :
:
Definičný obor: ![]()
Obor hodnôt: ![]()
Extrémy: nemá maximum ani minimum
Kde rastie a kde klesá: rastie všade
Prostosť funkcie: funkcia je prostá
Vlastnosti funkcie ![]() :
:
Definičný obor: ![]()
Obor hodnôt: ![]()
Extrémy: nemá maximum ani minimum
Kde rastie a kde klesá: klesá všade
Prostosť funkcie: funkcia je prostá
Rovnaké vlastnosti budú mať aj ostatné funcie, v ktorých ![]() bude nepárne číslo.
bude nepárne číslo.