Pascalov trojuholník

23.1.2020MatematikakombinatorikaTibor Menyhért

Blaise Pascal

Hoci sa Pascalov trojuholník nazýva podľa matematika Blaise Pascala, neobjavil ho on, ale poznali ho už v 13. storočí čínski matematici. Pascal však tento trojuholník a vzťahy ktoré v ňom platia preštudoval do hĺbky a tak bol pomenovaný po ňom.

Ako vytvoríme Pascalov trojuholník?

Do nultého riadku napíšeme 1, do prvého dve jednotky tak, že jednotka z predchádzajúceho riadku je v strede medzi nimi. Na začiatok a koniec každého ďalšieho riadku napíšeme jednotku a na ostatné pozície napíšeme súčet čísel, ktoré sú nad ním vľavo a vpravo. Tak ako ukazuje animovaný obrázok:

Možno dokázať, že jednotlivé čísla Pascalovho trojuholníka zodpovedajú kombinačným číslam.

n

$\sum$

0

${0 \choose 0}$

$2 ^ 0=1$

n=1

${1 \choose 0}$

${1 \choose 1}$

$2 ^ 1=2$

n=2

${2 \choose 0}$

${2 \choose 1}$

${2 \choose 2}$

$2 ^ 2=4$

n=3

${3 \choose 0}$

${3 \choose 1}$

${3 \choose 2}$

${3 \choose 3}$

$2 ^ 3=8$

n=4

${4 \choose 0}$

${4 \choose 1}$

${4 \choose 2}$

${4 \choose 3}$

${4 \choose 4}$

$2 ^ 4=16$

n=5

${5 \choose 0}$

${5 \choose 1}$

${5 \choose 2}$

${5 \choose 3}$

${5 \choose 4}$

${5 \choose 5}$

$2 ^ 5=32$

Vlastnosti Pascalovho trojuholníka

Pascalov trojuholník je osovo súmerný podľa osi prechádzajúcej horným vrcholom.
Súčet čísel v každom riadku zodpovedá n-tej mocnine čísla 2.
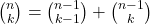${n \choose k}= {n-1 \choose k-1}+ {n-1 \choose k}$ pre $n > 0$

print

Pridaj komentár Zrušiť odpoveď