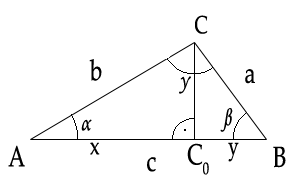
Majme trojuholník ABC, z vrcholu C veďme výšku na stranu c, ako ilustruje obrázok vpravo. Výška ![]() rozdelila trojuholník na dva pravouhlé trojuholníky
rozdelila trojuholník na dva pravouhlé trojuholníky ![]() a
a ![]() .
.
Pre oba trojuholníky platí Pytagorova veta:
![]()
![]()
![]()
![]()
![]()
![]()
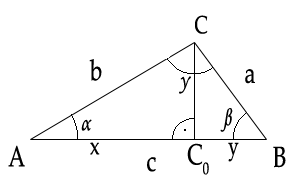
Majme trojuholník ABC, z vrcholu C veďme výšku na stranu c, ako ilustruje obrázok vpravo. Výška ![]() rozdelila trojuholník na dva pravouhlé trojuholníky
rozdelila trojuholník na dva pravouhlé trojuholníky ![]() a
a ![]() .
.
Pre oba trojuholníky platí Pytagorova veta:
![]()
![]()
![]()
![]()
![]()
![]()
Jeden robotník vykope 20 metrový kanál za 8 hodín. Za koľko hodín ho vykopú dvaja robotníci, ak sú rovnako výkonní?
Dvaja robotníci kanál vykopú dvakrát rýchlejšie, takže ho vykopú za 4 hodiny.
Auto išlo priemernou rýchlosťou 60 km za hodinu, z obce Pršany do obce Dažďany došlo za 1 hodinu. Na bicykli cyklista dosahuje na tej istej trati rýchlosť 20 km za hodinu, ako dlho mu cesta potrvá?
Cyklista ide trikrát pomalšie, cesta mu bude trvať trikrát tak dlho. Trasu prejde za tri hodiny.
Oba vyššie uvedené príklady boli príklady nepriamej úmernosti.
Nepriama úmernosť medzi dvoma veličinami je, ak vzťah medzi nimi možno vyjadriť vzorcom: ![]() , kde k je konštanta úmernosti a
, kde k je konštanta úmernosti a ![]()
Keď nakupujem rožky v obchode a jeden rožok stojí 8 centov, výsledná cena, ktorú zaplatím sa dá vyjadriť vzťahom: ![]() , kde c je cena a r je počet rožkov.
, kde c je cena a r je počet rožkov.
| Rožky | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Cena v centoch | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
Ak idem na bicykli konštantnou rýchlosťou 16 km za hodinu, dráha ktorú prejdem za nejaký čas sa dá vyjadriť vzťahom ![]() , kde s je dráha, a t je čas.
, kde s je dráha, a t je čas.
| Čas | 0 min | 15 min | 30 min | 1 hod | 2 hod | 3 hod |
| Dráha | 0 km | 4 km | 8 km | 16 km | 32 km | 48 km |
Poznámka: 15 minút je štvrť hodiny.
Hore uvedené vzťahy boli príklady priamej úmernosti.
Priama úmernosť medzi dvoma veličinami je, ak hodnotu závislej premennej od nezávislej premennej možno vyjadriť vzorcom v tvare: ![]() , kde
, kde ![]() . Konštanta priamej úmernosti k, je kladné reálne číslo.
. Konštanta priamej úmernosti k, je kladné reálne číslo.
Majme stanovený systém podmienok (napr. máme pravidelnú hraciu kocku, ktorej steny sú označené číslami 1, 2, . . . , 6). Proces (dej), ktorý môže nastať pri realizácii týchto podmienok (napr. hod hracou kockou) nazývame pokus. Vyžadujeme, aby každý pokus mal vlastnosť hromadnosti, t. j. aby sme ho mohli teoreticky ľubovoľne krát opakovať. Výsledok tohto procesu nie je jednoznačný, je náhodný, nazývame ho náhodným javom alebo náhodnou udalosťou (napr. padnutie šestky). Náhodný jav je výsledok pokusu. Množinu všetkých navzájom sa vylučujúcich výsledkov pokusu označujme gréckym písmenom ![]() . Jej prvky nazývame elementárne udalosti a označujeme ich písmenom
. Jej prvky nazývame elementárne udalosti a označujeme ich písmenom ![]() , t.j.
, t.j. ![]() . Podmnožiny množiny všetkých možných výsledkov pokusu nazývame náhodnými udalosťami.
. Podmnožiny množiny všetkých možných výsledkov pokusu nazývame náhodnými udalosťami.
Niektoré javy sú také, že vieme dopredu s absolútnou istotou povedať, čo sa stane za daných okolností:
Iné javy sú také, že nevieme s istotou povedať čo nastane, ale vieme že nastane niektorá z možností:
Prvú triedu nazývame deterministické javy. Druhú triedu javov nazývame náhodné javy.
V praxi neraz budete tovar preceňovať. Buď ho o nejaké percentá zdražíte alebo zlacníte, alebo zmenu vypočítate pripočítaním alebo odpočítaním nejakej čiastky a spätne budete potrebovať zistiť o koľko percent ste cenu zvýšili alebo znížili.
Zlacnenie: Ak tovar chceme zlacniť o p%, novú cenu vypočítame zo vzorca: ![]() kde
kde ![]() je nová cena a
je nová cena a ![]() je pôvodná cena.
je pôvodná cena.
Príklad: Tovar stoji 70 euro, zlacníme ho 20%. Aká bude nová cena?![]()
Nová cena bude 56 euro.
Zdraženie: Ak tovar chceme zdražiť o p%, novú cenu vypočítame zo vzorca ![]() kde
kde ![]() je nová cena a
je nová cena a ![]() je pôvodná cena.
je pôvodná cena.