Mocninové funkcie

6.11.2019MatematikaTibor Menyhért Leave a comment

Mocninová funkcia je funkcia v tvare: $y=a\cdot x^n,\, kde\, a\neq 0, n\neq 0,\,a,n,x \in R$

Kmitavý pohyb

25.10.2019FyzikaTibor Menyhért Leave a comment

Kmitavý pohyb je pohyb, ktorý sa pravidelne opakuje.

Zariadenia vykonávajúce pravidelne sa opakujúci pohyb:

a) kyvadlo
b) teleso zavesené na pružine
c) tyč upevnená na jednom konci
d) kvapalina v trubici v tvare U
e) hodinový nepokoj
f) struna

Kyvadlo. Rýchlosť, zrýchlenie, uhol výchylky

Kmitavý pohyb môže byť:

a) priamočiary
b) krivočiary
c) otáčavý
d) nerovnomerný (nerovnomerný je vždy)

Kmit: periodicky sa opakujúca sa časť kmitavého pohybu

Doba kmitu (perióda): doba, za ktorú sa vykoná jeden kmit. Značka: T

Frekvencia (kmitočet): Počet kmitov za sekundu. Značka: f

Prevod odmocnín na mocniny

24.10.2019MatematikaTibor Menyhért Leave a comment

Odmocňovanie je opačná operácia k umocňovaniu. $\sqrt[n]{a^n}=a$ .

Opačnou operáciu k sčítaniu je odčítanie a zistili sme, že odčítanie sa dá previesť na sčítanie. K číslu pripočítame záporné číslo:

$a-b=a+(-b)$

Podobne delenie je opačnou operáciu k násobeniu a zistili sme, že delenie sa dá previesť na násobenie: $a:b=a\cdot \dfrac{1}{b}$

Analogicky by mohlo platiť, že by sme nejako mohli previesť odmocňovanie na umocňovanie.

Continue reading →

Odmocniny

23.10.2019MatematikaTibor Menyhért Leave a comment

Druhá odmocnina z a je také číslo b pre ktoré platí:

$a=b \cdot b$ označujeme ho $b= \sqrt a$

Odmocňovanie je opačná operácia k umocňovaniu, takže platí:

$\sqrt { a^2 }=a$

Podobne možno zadefinovať tretiu odmocninu:

Tretia odmocnina z a je také číslo b pre ktoré platí:

$a=b \cdot b \cdot b$ označujeme ho $b= \sqrt[3]{a}$

Všeobecne: n-tá odmocnina z a je také číslo b pre ktoré platí:

$a=b^n$ označujeme ho $b= \sqrt[n]{a}$

Platí: $\sqrt[n]{a^n}=a$

Continue reading →

Mocniny čísla desať. Zápis veľmi veľkých a veľmi malých čísel

23.10.2019MatematikaTibor Menyhért Leave a comment

Mocniny čísla 10:

$10^0=1\hspace{15}10^1=10 \hspace{15} 10^2=100 \hspace{15} 10^3=1000 \hspace{15} 10^4=10000$

$10^ 5=100000 \hspace{15} 10^ 6=1000000$

$10^{-1}=0,1 \hspace{15} 10^{-2}=0,01 \hspace{15} 10^{-3}=0,001$

Počítame v desiatkovej sústave. Čislo 3456 možno zapísať v tvare:

$3456=3\cdot 1000+ 4\cdot 100+5 \cdot 10+ 6\cdot 1$

Čísla 1, 10, 100, 1000 sú mocniny čísla 10, takže toto číslo môžeme zapísať aj v tvare:

$3456=3\cdot 10^3+ 4\cdot 10^2+5 \cdot 10^1+ 6\cdot 10^0$

Podobne aj desatinné čísla môžeme zapísať ako súčet mocnín čísla desať:

$0,5607=5\cdot 10^{-1}+ 6\cdot 10^{-2} +0 \cdot 10^{-3}+ 7\cdot 10^{-4}$

Niekedy spracujeme s veľmi veľkými alebo s veľmi malými číslami. Často je pohodlnejšie takéto čísla zapísať v tvare súčinu nejakého čísla a mocniny desiatky. Napríklad číslo: 1 235 000 000 – jedna miliarda 235 miliónov možno zapísať takto:

$123500000=1,235 \cdot 10^{9 }$

Alebo číslo $0,000000005627=5,627 \cdot 10^{-9}$

Continue reading →

Mocniny

21.10.2019MatematikaTibor Menyhért Leave a comment

Už na základnej škole ste sa stretli s druhou a treťou mocninou a so zovšeobecnením pre umocňovanie na ľubovolné prirodzené číslo.

Druhá mocnina: $a^2=a\cdot a$

Druhu mocninu ste používali napríklad pri výpočte obsahu štvorca a kruhu a pri Pytagorovej vete.

Obsah štvorca so stranou $a$ : $S=a^2$

Obsah kruhu s polomerom $r$ : $S=\pi r^2$

Pytagorova veta: $c^2=a^2+b^2$

Tretia mocnina: $a^3=a\cdot a \cdot a$

Tretiu mocninu ste používali napríklad pri výpočte objemu kocky a objemu gule.

Objem kocky so stranou $a$ : $V=a^3$

Objem gule s polomerom $r$ : $V=\dfrac{4}{3}\pi r^3$

n-tá mocnina

Zovšeobecnením môžeme zaviesť mocninu na n:

$a^n=a_1\cdot a_2\cdot ... \cdot a_n,\, kde\, a_1=a_2=...=a_n$

Súčin n rovnakých činiteľov nazývame n-tá mocnina.

Pravidlá pre počítanie s mocninami

Možno dokázať nasledujúce pravidlá pre počítanie s mocninami:

$a^n \cdot a^m= a^{m+n}$
$a^n : a^m= a^{m-n}$
$(a^m)^n=a^{m \cdot n}$
$(a\cdot b)^n=a^n \cdot b^n$
$\begin{pmatrix}\dfrac{a}{b}\end{pmatrix}^n=\dfrac{a^n}{b^n}$

Dôkazy nájdete v tomto článku (zatiaľ nenapísané)

Príklady:

$0^n=0, \,ak \, n\,\neq 0$

$1^n=1$

$\begin{tabular}[p]{2} 2^2=4 \hspace{15} 2^3=8\\ 3^2=9 \hspace{15} 3^3=27\\ 4^2=16 \hspace{15} 4^3=64\\ 5^2=25 \hspace{15} 5^3=125\\ 6^2=36 \hspace{15} 6^3=216\\ 7^2=49 \hspace{15} 7^3=343\\ 8^2=64 \hspace{15} 9^3=512\\ 9^2=81 \hspace{15} 9^3=729\\ 10^2=100 \hspace{15} 10^3=1000\\ \end{tabular}$

$30^2=(3.10)^2=3^2\cdot 10^2=9 \cdot 100=900$ Vzorec: $(ab)^n=a^n \cdot b^n$

Čo je prvá mocnina?

$a^{m+1}:a^m=a^{m+1-m}=a^1=a$

Použili sme vzorec pre delenie mocnín s rovnakým základom $a^m:a^n=a^{m-n}$ a skutočnosť, že v čitateľovi sa $a$ nachádza o jeden raz častejšie než v menovateľovi, takže po vykrátení nám zostane len $a$ .

Čo je nultá mocnina?

$a^n:a^n=a^{n-n}=a^0=1, a\neq0$

Znova sme použili vzorec $a^m:a^n=a^{m-n}$ a skutočnnosť, že podiel dvoch rovnakých čísel je 1.

Čo sú záporne celé mocniny?

$a^0:a^n=a^{0-n}=a^{-n}=\dfrac{1}{a^n}, a\neq 0$

Príklady:

$2^{-1}=\dfrac{1}{2}=0,5$

$2^{-2}=\dfrac{1}{2^2}=\dfrac{1}{4}=0,25$

$\left( \dfrac{2}{3} \right) ^{-2}=\dfrac{1}{(\frac{2}{3})^2}=\dfrac{3^2}{2^2}=\dfrac{9}{4}=2,25$

Premeny jednotiek

17.10.2019Fyzika, MatematikaTibor Menyhért Leave a comment

Keď je nameraná veličina výrazne väčšia alebo menšia než jednotka veličiny, zvykneme je uviesť vo väčších alebo menších jednotkách, musíme preto poznať spôsob prevodu na väčšie alebo menšie jednotky.

Continue reading →

Číselné množiny

16.10.2019MatematikaTibor Menyhért Leave a comment

Prirodzené čísla: Čísla, ktoré označujú počet alebo poradie nazývame prirodzené čísla. Množinu prirodzených čísel označujeme písmenom N.

Podľa tejto definície je aj nula prirodzené číslo, niektoré matematické kurzy nulu za prirodzené číslo nepovažujú.

$\frac{a}{b}$ kde $a,b\in Z \, b\neq 0$ .

Čísla označujúce poradie sa tiež nazývajú ordinálne čísla (z angl. order).
Čísla označujúce počet prvkov množiny, respektíve veľkosť množiny sa tiež nazývajú kardinálne čísla.

Súčet dvoch prirodzených čísel je prirodzené číslo. Množina prirodzených čísel je vzhľadom na operáciu sčítania uzavretá.

Množina prirodzených čísel nie je vzhľadom na operáciu odčítania uzavretá. Napríklad 2-3 nie je prirodzené číslo. Ak chceme zadefinovať množinu, ktorá je vzhľadom na operáciu odčítania uzavretá, dospejeme k pojmu množina celých čísel.

Celé čísla: Celé čísla sú zjednotením množiny prirodzených čísel a čísel k nim opačných. Opačné číslo k číslu a je -a. K -a dospejeme aj takto 0-a=-a. Súčet opačných čísel je nula. Množinu celých čísel označujeme písmenom Z.

Množina celých čísel je uzavretá vzhľadom na operácie: sčítanie, odčítanie a násobenie. Ak chceme, aby sme dostali množinu, ktorá je uzavretá aj na operáciu delenie, dospejeme k množine racionálnych čísel.

Racionálne čísla: Racionálne čísla sú čísla, ktoré možno vyjadriť v tvare zlomku:

$\frac{a}{b}$ kde $a,b\in Z \, b\neq 0$ .

Racionálne čísla označujeme písmenom Q.

Množina racionálnych čísel je uzavretá vzhľadom na operácie: sčítanie, odčítanie, násobenie a delenie s výnimkou delenia nulou. Ak si zavedieme operácie umocňovanie a k nej opačnú (inverznú operáciu) odmocňovanie, tak zistíme, že množina racionálnych čísel znova nie je uzavretá vzhľadom na operáciu odmocňovanie. Keď však zostrojíme štvorec so stranou 1, tak vidíme, že existuje úsečka, ktorá má dĺžku $\sqrt{2}$ . je to uhlopriečka tohto štvorca. Možno pritom dokázať, že $\sqrt{2}$ nemožno vyjadriť v tvare zlomku. Takto dospejeme k pojmu množina reálnych čísel.

Reálne čísla: Reálne čísla sú čísla, ktoré možno zobraziť na číselnej osi. Reálne čísla sú dĺžky všetkých úsečiek. Reálne čísla označujeme písmenom R.

Iracionálne čísla: Reálne čísla, ktoré nie sú racionálne nazývame iracionálne čísla. Nedajú sa vyjadriť v tvare zlomku dvoch celých čísel.

Pre horeuvedené číselné množiny platí:

$N\subset Z \subset Q \subset R$

Slovom N je podmnožinou Z, Z je podmnožinou Q a Q je podmnožinou R.

Množiny a operácie s množinami

16.10.2019MatematikaTibor Menyhért Leave a comment

Množina je súbor objektov o ktorých vieme rozhodnúť, či do množiny patria.
Množiny obvykle označujeme veľkými písmenami.

Prvok množiny: Objekt, ktorý do množiny patrí, nazývame prvok množiny.

Prvky množiny obvykle označujeme malými písmenami.

Výraz $p\in A$ čítame ako p je prvkom A.

Výraz $p\notin A$ čítame ako p nie je prvkom A.

Podmnožina: Ak pre každý prvok množiny A platí, že je prvkom množiny B množina A je podmnožinou B

Výraz $A\subseteq B$ čítame ako A je podmnožinou B.

Vlastná podmnožina: Ak existuje aspoň jeden prvok množiny B, ktorý nie je prvkom A a A je podmnožinou B, potom A je vlastnou podmnožinou B.

Značíme výrazom: $A\subset B$

Grafické vyjadrenie podmnožiny

Príklady množín a ich podmnožín:

množina cicavcov je podmnožinou množiny zvierat
množina zvierat je podmnožinou množiny živočíchov
množnina párnych čísel je podmnožinou celých čísel
množina dravcov nie je podmnožinou množiny cicavcov – existujú aj dravé vtáky a dravé ryby
množina žiakov triedy je podmnožinou žiakov školy

Nadmnožina: Ak množina A obsahuje všetky prvky množiny B, množinu A nazývame nadmnožina množiny B.

Prázdna množina: Množina, ktorá nemá prvky sa nazýva prázdna množina.

Značíme buď { } alebo $\emptyset$

Množinu môžeme určiť troma spôsobmi:

vymenovaním prvkov
uvedením vlastností, ktoré majú prvky spĺňať
množinovými operáciami

a kombináciou hore uvedených spôsobov.

Operácie s množinami

Zjednotenie množín: Zjednotením množiny A a množiny B je množina všetkých prvkov, ktoré sú prvkami množiny A alebo množiny B.

Značíme: $A\cup B$

Zjednotenie množín môžeme zapísať v tvare $A\cup B= \{\forall p, \, p\in A \, \lor\, p \in B\}$

Poznámka: $\lor$ je logická spojka alebo.

Graficky možno zjednotenie vyjadriť pomocou Vennovho diagramu:

Prienik množín: Prienikom množiny A a množiny B je množina všetkých prvkov, ktoré sú prvkami množiny A a množiny B.

Značíme: $A\cap B$

Prienik množín môžeme zapísať v tvare: $A\cap B= \{\forall p, \, p\in A \, \land\, p \in B\}$

Poznámnka: $\land$ je logická spojka a.

Grafické vyjadrenie prieniku množín Vennovym diagramom

Rozdiel množín: Rozdiel množín A a B je množina všetkých prvkov, ktoré patria do A a nepatria do B.

$x \in A - B \Leftrightarrow (x \in A \land x \notin B)$

Vennov diagram rozdielu množín

Zdroje

Obrázky sú prevzaté z wikipédie.

https://sk.wikipedia.org/wiki/Rozdiel_mno%C5%BE%C3%ADn

https://sk.wikipedia.org/wiki/Prienik_(matematika)

https://sk.wikipedia.org/wiki/Zjednotenie_(matematika)

Počítanie so zlomkami

15.10.2019MatematikaTibor Menyhért Leave a comment

V živote sa často stretávame so situáciou, keď je celok rozdelený na niekoľko rovnakých častí. Napríklad pizza, čokoláda, bomboniera s rovnakými cukríkmi, …

Matematika by mala poskytovať aparát, ktorý umožňuje počítať s takýmito časťami celku. Časť celku, či viacero rovnakých častí celku nazývame zlomok.

Zlomok je číslo v tvare $\hspace{10}\dfrac{a}{b}\hspace{10} a,b \in Z \hspace{15} b\neq 0$

$Z$ je množina celých čísel, $\in$ je znak patrí do množiny. Vyššie uvedený výraz možno prečítať $a, b$ sú celé čísla a $b$ sa nerovná nula.

Číslo nad zlomkovou čiarou nazývame čitateľ, číslo pod zlomkovou čiarou nazývame menovateľ, čiara medzi čitateľom a menovateľom je zlomková čiara.

Krátenie zlomku

Ak čitateľa i menovateľa predelíme tým istým číslom rôznym od nuly, hodnota zlomku sa nezmení. Nazývame to krátenie zlomku. Napríklad: $\dfrac{2}{4}=\dfrac{2\cdot{}1}{2\cdot{}2}=\dfrac{1}{2}$

Rozšírenie zlomku

Ak čítateľa i menovateľa vynásobíme tým istým číslom rôznym od nuly, hodnota zlomku sa nezmení. Nazývame to rozšírenie zlomku. Npríklad: $\dfrac{3}{4}=\dfrac{3\cdot{}3}{4\cdot{3}}=\dfrac{9}   Sčítanie zlomkov   a) s rovnakými menovateľmi   Zlomky s rovnakým menovateľom sčítame tak, že menovateľa opíšeme a čitateľov sčítame  $ \dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} $  b) s rôznymi menovateľmi   Zlomky prevedieme na rovnakého menovateľa a potom postupujeme ako v prípade a)  $ \dfrac{a}{b}+\dfrac{c}{d}= \dfrac{a\cdot d}{b \cdot d} +\dfrac{c\cdot b}{d\cdot b}=\dfrac{a \cdot d+c \cdot b}{b \cdot d} $  Prvý zlomok sme rozšírili číslom d a druhý číslom b. Najjednoduchšie je previesť menovateľov na ich najmenší spoločný násobok, ale aj hore uvedený spôsob vedie k správnemu výsledku.   Mnemotechnickou pomôckou je krížové pravidlo, podľa nasledujúceho obrázku:   <figure class="wp-block-image size-full is-resized"><img src="https://evyuka.sk/wp-content/uploads/2023/04/kpravidlo.jpg" alt="" class="wp-image-3198" width="846" height="635"/><figcaption class="wp-element-caption">Prvého čitateľa vynásobime druhým menovateľom, druhého čitateľa prvým menovateľov, tieto výsledky sčítame a do menovateľa dáme súčin menovateľov.</figcaption></figure>   Odčítanie zlomkov   a) s rovnakými menovateľmi   Zlomky s rovnakým menovateľom odčítame tak, že menovateľa opíšeme a od prvého čitateľa odpočítame druhého čitateľa  $ \dfrac{a}{c}-\dfrac{b}{c}=\dfrac{a-b}{c} $  b) s rôznymi menovateľmi   Zlomky prevedieme na rovnakého menovateľa a potom postupujeme ako v prípade a)  $ \dfrac{a}{b}-\dfrac{c}{d}= \dfrac{a\cdot d}{b \cdot d} -\dfrac{c\cdot b}{d\cdot b}=\dfrac{a \cdot d-c \cdot b}{b \cdot d} $  Násobenie zlomkov   Zlomky násobime tak, že čitateľa vynásobime čitateľom a menovateľa menovateľom.  $ \dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{a\cdot c}{b \cdot d} $  Delenie zlomkov   Zlomky delíme tak, že druhý zlomok prevrátime (čitateľ sa stane menovateľom a naopak) a tieto zlomky vynásobime.  $ \dfrac{a}{b}:\dfrac{c}{d}= \dfrac{a}{b} \cdot \dfrac{d}{c} = \dfrac{a \cdot d}{b \cdot c} $  Ak budeme mať zložený zlomok, tak ide vlastne tiež o delenie zlomku zlomkom a postupujeme rovnako alebo rovno výnasobíme vonkajšie hodnoty a zapíšeme do čitateľa a vnútorné hodnoty a zapíšeme do menovateľa.  $ \dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}= \dfrac{a \cdot d}{b \cdot c} $  Príklady  $ \dfrac{1}{2}+\dfrac{1}{3}=\dfrac{1\cdot 3}{2\cdot 3}+ \dfrac{1\cdot 2}{3\cdot 2} =\dfrac{3+2}{6}=\dfrac{5}{6} $ $ \dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1\cdot 3}{2\cdot 3}- \dfrac{1\cdot 2}{3\cdot 2} =\dfrac{3-2}{6}=\dfrac{1}{6} $ $ \dfrac{1}{2}\cdot \dfrac{1}{3}=\dfrac{1 \cdot 1}{2 \cdot 3}=\dfrac{1}{6} $ $ \dfrac{1}{2}: \dfrac{1}{3}= \dfrac{1}{2}\cdot \dfrac{3}{1}=\dfrac{3}{2}=1,5 $  Poznámka: Výsledok sme mohli nechať aj v tvare$ \dfrac{3}{2} $  $ \dfrac{2}{3}\cdot \left( \dfrac{2}{5}+\dfrac{3}{7}\right)= \dfrac{2}{3}\cdot \dfrac{2 \cdot 7+3\cdot 5 }{5\cdot 7 }= \dfrac{2}{3}\cdot \dfrac{29}{35}=\dfrac{58}{105} $  Čo je väčšie?$ \dfrac{1}{3} alebo \dfrac{2}{7} $  Riešenie 1: Prevedieme na spoločného menovateľa a zlomok, ktorý bude mať väčšieho čitateľa bude väčší.   Spoločný menovateľ je 21.$ \dfrac{1}{3}=\dfrac{7}{21}\hspace{15} \dfrac{2}{7}=\dfrac{6}{21} $teda$ \dfrac{1}{3}>\dfrac{2}{7} $  Riešenie 2: Zlomky rozšírime tak, že čitatelia budú rovnakí. Zlomok, ktorý bude mať menšieho menovateľa bude väčší.  $ \dfrac{1}{3}=\dfrac{2}{6} $teda$ \dfrac{1}{3}>\dfrac{2}{7}$

Poznámka: Výhodou prvého riešenia je, že vieme o koľko je 1/3 väčšia než 2/7, výhodou druhého je, že sme to vypočítali rýchlejšie.

Zaokrúhľovanie

14.10.2019MatematikaTibor Menyhért Leave a comment

Niekedy stačí, ak výsledok výpočtu zobrazíme na istý počet miest. Výsledok môžeme zaokrúhliť.

Pravidlá zaokrúhľovania:

Zaokrúhlenie nadol: Ak prvá číslica, ktorú máme zaokrúhliť je menšia ako 5, predchádzajúce číslice opíšeme a zaokrúhlenú číslicu a všetky číslice za ňou vynecháme.
Zaokrúhlenie nahor: Ak prvá číslica, ktorú máme zaokrúhliť je väčšia ako 4, k predchádzajúcej číslici pripočítame jednotku a zaokrúhlenú číslicu a číslice za ňou vynecháme.

Znakom zaokrúhlenia je znak rovná sa a nad ním krúžok alebo bodka: $\doteq$

Continue reading →

AI. Projekt Mlyn

20.6.2018InformatikaApp Inventor, mlynTibor Menyhért Leave a comment

Mlyn sa hrá na hracom pláne, aký je na obrázku vpravo.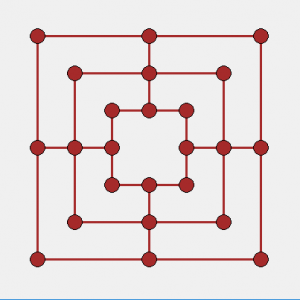

Pravidlá:

Na začiatku hry je hrací plán prázdny, obaja hráči majú po 12 kameňov
Striedavo prikladajú na kruhy hracieho plánu kamene, ak hráč vytvorí trojicu vedľa seba ležiacich kameňov rovnakej farby (mlyn), súperovi vezme ľubovoľný kameň, ktorý nie je súčasťou mlynu
Keď boli položené všetky kamene, hráči môžu kamene posúvať po líniách o jedno políčko, ak je políčko voľné.
Ak má hráč iba tri kamene, môže kameňmi skákať na ľubovoľné voľné políčko
Prehráva hráč, ktorému zostanú dva kamene

Continue reading →

Excel. Voľby do NR SR. 1. skrutínium. Vzorce

28.5.2018InformatikaexcelTibor Menyhért Leave a comment

Na internete vyhľadajte, aký je volebný systém do Národnej rady Slovenskej republiky
Na základe preštudovania tohto systému vytvorte odhad počtu mandátov pre jednotlivé strany v prvom skrutíniu, ak by počet platných hlasov bol 2000000 a voľby by dopadli presne podľa výsledkov prieskumu.

Pojmy, ktoré pri vytvorení vzorcov budete potrebovať:

volebný prah
volebné číslo
celkový počet mandátov v NR SR
1. skrutínium

Excel. Voľby do NR SR. Grafy

28.5.2018InformatikaexcelTibor Menyhért Leave a comment

Vyhľadajte na internete najnovší prieskum volebných preferencií agentúry AKO a výsledky prieskumu zadajte do excelovskej tabuľky.
Vytvorte koláčový graf preferencií.
Vyhľadajte aj predchádzajúce výsledky prieskumov tej istej agentúry a vytvorte čiarový graf pre jednotlivé strany, ako sa vyvíjali ich preferencie v čase (aspoň tri prieskumy)

Test – počítačová terminológia

3.5.2018Informatikaangličtina, testTibor Menyhért Leave a comment

Kliknite na túto adresu

AI. Projekt Krtko

10.4.2018InformatikaApp InventorTibor Menyhért Leave a comment

Vašou úlohou bude naprogramovať jednoduchú hru Krtko.

Na obrazovke sa každú sekundu objaví krtko na náhodnej pozícií, úlohou hráča je kliknúť na krtka, ak hráč krtka trafí, pripočítajú sa mu body a krtko sa objaví na novej pozícii, ak netrafí, zvýši sa hodnota mimo, ak hráč v stanovenom limite na krtka neklikne, krtko sa premiestni inam a zvýši sa hodnota pozde.

Continue reading →

App Inventor. Projekt Grafický editor

1.2.2018InformatikaApp InventorTibor Menyhért Leave a comment

Vytvorme jednoduchý grafický editor, ktorý bude kresliť čiary a malé a veľké bodky, v ktorom bude možné nastaviť farbu pera, mazať nakreslený obrázok, ktorý bude alebo nebude mať pozadie a v ktorom bude používateľ môcť urobiť fotku a táto fotka sa stane pozadím. Naučíte sa pracovať s prvkami Canvas (plátno), Camera (fotoaparát, kamera), Variables (premenné) … Continue reading →

App Inventor. Projekt Kocúr

29.1.2018InformatikaApp InventorTibor Menyhért Leave a comment

Úloha: Vytvorte projekt Kocur (krátke u nie je preklep, v AI v názvoch objektov nemožno používať diakritiku). Na obrazovke telefónu bude obrázok kocúra, ak naň klikneme, kocúr zamňauká. Ak prst na kocúrovi podržíme, kocúr bude priasť (telefón zavibruje). Keď mobilom zatrasieme, kocúr bude prskať.

Po vytvorení nového projektu New project sa zobrazí nasledujúca stránka:

Vľavo sú ovládacie prvky, v strede dizajn aplikácie, napravo zoznam použitých prvkov a celkom vpravo vlastnosti aktuálneho objektu.

Najprv umiestnime na obrazovku telefónu pokyn, ako má používateľ aplikáciu ovládať. Presunieme kurzor na prvok Label (nápis, návestie, štítok). Myšou ho presunieme na telefón, upravíme vlastnosti nápisu: zväčšíme veľkosť písma (FontSize) , farbu pozadia (BackgroundColor), farbu textu (TextColor), zmažeme text a nahradíme ho textom Pohlaďte kocúra.

Potrebujeme aplikácii sprístupniť dva súbory: obrázok kocúra a zvuk, ktorý vydáva. Kliknite na Média pre projekt kocúr, celkom dole kliknite na kitty.png, súbor stiahnite do počítača, potom kliknite na meow.mp3 a tiež ho stiahnite do počítača. Môžete tiež vyhľadať obrázok kocúra na internete a vyhľadať iné mňaučanie.

Presuňte na telefón prvok Button (tlačítko), vo vlastnostiach kliknite na Image (obrázok), otvorí sa nové okno, kliknite na UploadFile (nahraj súbor) a z priečinka kam sa uložili súbory kitty.png a meow.mp3 nahrajte súbor kitty.png. Tlačítko sa zmenilo na kocúra. Stredom tlačítka prechádza nápis, postavte sa vo vlastnostiach tlačítka na Text a text zmažte.

V ľavej sekcii prejdite na položku Media, vyberte prvok Sound a presuňte ho na telefón. Sound sa v telefóne nezobrazí, zobrazí sa pod ním medzi Non-visible component (neviditeľné prvky). Vo vlastnostiach kliknite na Source (zdroj), potom na UploadFile a nahrajte súbor meow.mp3.

Dizajnovú časť máte predbežne hotovú. Prejdite k programovaniu aplikácie. Vpravo hore kliknite na Blocks. Zobrazia sa dve sekcie, vľavo je sekcia Blocks (bloky), vpravo sekcia Viewer (zobrazovač, náhľad). Kliknutím na Button1 sa zobrazia nasledujúce bloky:

Hnedé bloky predstavujú udalosti, ktoré môžu s tlačítkom nastať. Prvý when Button1.Click (keď je tlačítko stlačené) je ten, ktorý potrebujete. Postavte sa naň, držte stlačené tlačítko myši a presuňte ho do sekcie Viever. Keď klikneme na Button1, má sa ozvať mňaukanie, kliknite v sekcii Blocks na Sound1, zobrazí sa:

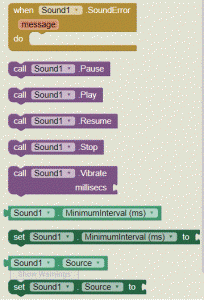
Je tu jedna udalosť a niekoľko akcií, ktoré možno so zvukom robiť. Chcete prehrať zvuk, vyberte blok Call Sound1.Play a presuňte ho do bloku When Button1.Click. Ďalej chceme, aby kocúr nielen mňaukal, ale aj priadol (vibroval). Vyberieme blok When Button1.longClick, presuňte blok call Sound1.Vibrate do bloku longClick. Tento blok má výrez, kam pre blok s počtom milisekúnd, ako dlho má mobil vibrovať. Potrebujete blok s číslom, čísla súvisia s matematikou, kliknite na položku Math a prvý blok je číslo, presunieme ho do výrezu a nastavíme napríklad číslo 500.

Aplikácia je hotová, potrebujeme ju skompilovať, nájdite celkom hore položku Build, kliknite na ňu zobrazia sa možnosti App (provide QR code for Apk) a App (save .apk to my computer). Vyberte prvú položku, aplikácia sa preloží, po preklade sa zobrazí okienko s čiarovým kódom, keď kód zosnímete čítačkou čiarových kódov, stiahne sa súbor s vašou aplikáciou. Po stiahnutí súboru, kliknite na otvoriť, mobil vás možno upozorní, že takýto typ súboru môže poškodiť mobil, keďže ste aplikáciu sami vytvorili, je bezpečná, takže ju nainštalovať môžete.

Pokiaľ chceme, aby kocúr syčal, keď mobilom trasieme, vráťte sa do dizajnéra, v ľavej sekcii vyberte položku Sensors (senzory), potom AccelerometerSensor (senzor zrýchlenia), presuňte ho na mobil. Na internete vyhľadajte zvuk syčania mačky, stiahnite ho do počítača, na telefón presuňte blok Sound a uploudujte zvuk syčania. Znova otvorte Blocks, kliknite na AccelerometerSensor1, vyberte blok when AccelerometerSensor1.Shaking, kliknite na Sound2 a vyberte blok Play. Znova skompilujte aplikáciu a stiahnite ju čítačkou čiarového kódu.

Poznámka: Aby ste nemuseli aplikáciu stále kompilovať a inštalovať do telefónu, na Google play nájdite aplikáciu Mit AI2 Companion, keď ju na mobile spustíte a v prehliadači kliknete na Connect a Companion, zobrazí sa QR kód. Po jeho zosnímaní mobilom sa v mobile spustí simulácia aplikácie.

Námety na samostatnú prácu

aplikáciu môžete upraviť podľa vlastnej fantázie, môžete pridať tlačítko na ktorom bude pes a po kliknutí naň bude štekať, môžete pridať aj iné zvieratá a zvuky, ktoré vydávajú (obrázky a zvuky nájdite pomocou vyhľadávača)
ak máte psa alebo mačku, môžete ich odfotiť a nahrať zvuky, ktoré vydávajú
aplikáciu možno upraviť tiež tak, že používateľ môže odfotiť zviera a nahradiť obrázok, ktorý je v aplikácií vlastným obrázkom, to isté možno urobiť so zvukom
možno ju tiež upraviť do podoby kvízu, kliknutím na tlačítko sa ozve náhodný zvuk a používateľ má kliknúť na zviera, predmet, … , vydávajúci takýto zvuk
Aby ste sa v programovacej sekcii lepšie orientovali, je vhodné v Designer nazvať jednotlivé prvky podľa toho čo predstavujú. Button1 – Kocur, Sound1 – Mnau, …

Literatúra:

Článok bol napísaný na základe prvej kapitoly knihy App Inventor, Computer Press 2014

Dotazník

24.1.2018InformatikaTibor Menyhért Leave a comment

Klikni na tento odkaz

Test z informatiky

19.1.2018InformatikaTibor Menyhért Leave a comment

Test z informatiky 2 Continue reading →

Udalosti. Ovládacie prvky (tlačítko, vstupné pole, návestie)

16.1.2018InformatikaPythonTibor Menyhért Leave a comment

Používateľské rozhranie v grafickom režime vyžaduje niekoľko objektov, pomocou ktorých môže používateľ program ovládať. Najpoužívanejšie sú:

tlačítko (Button)
vstupné pole (Entry)
návestie (Label)

Ich konkrétne použitie si ukážeme pri programovaní matematickej hry Taxman. Continue reading →

Udalosti (tlačidlá)

16.1.2018InformatikaPythonTibor Menyhért Leave a comment

Štandardná myš má tri tlačidlá, môžeme jej v programe priradiť tri funkcie, ktoré sa vykonajú po ich stlačení. Geometrických tvarov, ktoré by sme potrebovali kresliť je omnoho viac, potrebujeme preto nástroje, ktorými môžeme rozšíriť možnosti nášho grafického editora. Takýmto nástrojom je príkaz Button, ktorý vytvorí tlačidlo. Každému tlačidlu môžeme priradiť nejakú funkciu. Continue reading →

Udalosti (stlačenie tlačítka myši)

8.1.2018InformatikaPythonTibor Menyhért Leave a comment

Program by mal nejako reagovať na akcie používateľa. Jednou z akcií ktoré môže používateľ vykonať, je kliknutie ľavým, pravým alebo stredným tlačítkom myši. Continue reading →

Ukážkový formulár

21.12.2017InformatikaTibor Menyhért Leave a comment

Prosím vyplňte tento dotazník

Test úrovne informatického myslenia

18.12.2017InformatikaTibor Menyhért Leave a comment

Kliknite na túto adresu

Kyberšikana

15.12.2017Informatikak&beršikanaTibor Menyhért Leave a comment

Na tejto adrese nájdete prezentáciu o Kyberšikane

Scrable (1). Hrací plán (cyklus for a funkcie str a chr)

11.12.2017Informatikalogické hry, Python, Scrable, slovné hryTibor Menyhért Leave a comment

V projekte Scrable sa pokúsime naprogramovať slovnú hru Scrable. Popritom sa oboznámite so základnými príkazmi a vlastnosťami jazyka Python. Continue reading →

Vianočné hviezdy z papiera

6.12.2017Technická výchovapapierové výrobky, vianoceTibor Menyhért Leave a comment

Materiál a náradie:

list papiera A4 (biely alebo farebný)
nožnice
lepidlo
ceruzka

Continue reading →

Python. Tkinter. Nakreslenie mnohouholníka

28.11.2017InformatikaPythonTibor Menyhért Leave a comment

Mnohouholník nakreslíme príkazom create_polygon.

Prvé parametre sú súradnice vrcholov mnohouholníka. Ďalšie paramentre sú rovnaké, ako v iných grafických príkazoch, farba výplne – fill, farba vonkajších hrán – outline, hrúbka vonkajších hrán – width.

Príkaz: platno.create_polygon(100,100,300,100,300,200,fill=“pink“) nakreslí trojuholník vyplnený ružovou farbou. Continue reading →

Zmazanie frontu tlačiarne

24.11.2017InformatikaTibor Menyhért Leave a comment

Niekedy sa stáva, že vo fronte tlačiarne zostanú nejaké úlohy a nedajú sa zrušiť. Niekedy pomôže reštartovanie počítača, ale výnimočne sa stáva, že ani reštart počítača nepomáha.

Nasledujúci program by vám mal pomôcť: Printer Quee Cleaner

Tkinter. Práca s textom.

23.11.2017InformatikaPythonTibor Menyhért Leave a comment

Keď pracujeme s grafikou, často potrebujeme okrem grafických prvkov použiť aj text. Napísanie textu na plátno uskutočníme príkazom create_text. Continue reading →

Projekt Scrable (1)

19.11.2017Informatikalogické hry, Python, Scrable, slovné hryTibor Menyhért Leave a comment

Pri programovaní hry Scrable sa oboznámite s väčšinou základných vlastností jazyka Python. Z riešenia jednotlivých problémov automaticky vyplynie potreba funkcie, metódy či dátového typu, ktoré ešte nepoznáte . Continue reading →

Mlyn (Python) 1. Hrací plán

7.11.2017Informatikalogické hry, mlyn, PythonTibor Menyhért Leave a comment

Pokúsime sa v Pythone naprogramovať hru Mlyn. Pravidlá nájdete v článku Mlyn. Continue reading →

Python. Grafické príkazy. Modul tkinter

3.11.2017Informatikagrafika, PythonTibor Menyhért Leave a comment

Python je modulárny programovací jazyk. Základnú sadu príkazov možno rozšíriť rôznymi modulmi. Keď potrebujeme pracovať s grafikou, môžeme si vybrať z veľkého množstva modulov. Oboznámim vás s modulom tkinter.

Continue reading →

Animačné techniky

27.10.2017InformatikaTibor Menyhért Leave a comment

Animácia je zaznamenanie sekvencie obrázkov, ktoré sú samy o sebe statické a zobrazujú pohyb po malých krokoch. Pri rýchlom zobrazovaní obrázkov za sebou splynú do pohyblivého obrazu a to vďaka zotrvačnosti ľudského oka. Snímky sa však musia prehrávať takou rýchlosťou, ktorú ľudské oko nepostrehne.

Odkaz na stránku animuj

Odkazy na vylepšenú Elizu

26.10.2017InformatikaTibor Menyhért Leave a comment

Eliza 2

22.10.2017InformatikaPython, sémantika, syntax, umelá inteligenciaTibor Menyhért Leave a comment

Už úvodná Elizina otázka Ako sa voláš?, či skôr odpoveď používateľa, predstavuje komplikovaný problém. Niekto odpovie menom, niekto menom a priezviskom, ďalší priezviskom a menom, iný prezývkou v kombinácii s priezviskom či bez neho a ktosi odpovie svojim priezviskom. Ak by Eliza bola človek, vo väčšine prípadov by vedela identifikovať, o ktorý variant ide. Continue reading →

Eliza (umelá inteligencia?) 1

19.10.2017InformatikaPython, umelá inteligenciaTibor Menyhért Leave a comment

Žiaci 8. B prišli s nápadom, rozvinúť dialóg s programom tak, aby to neboli len otázky počítača človeku, ale aby aj človek mohol klásť otázky počítaču a aby to vyzeralo, ako skutočný dialóg medzi dvoma ľuďmi. Spomenul som si na program Eliza, ktorý bol pravdepodobne inšpirovaný Turingovým testom umelej inteligencie – program bude mať vlastnosti umelej inteligencie, keď človek pri dialógu s programom alebo s človekom nerozozná, či je na druhom konci človek alebo počítač. Continue reading →

Odkaz na program reťazce

16.10.2017InformatikaPythonTibor Menyhért Leave a comment

Klikni sem

Funkcie a metódy na prácu s reťazcami

10.10.2017InformatikaPythonTibor Menyhért Leave a comment

len(r) – Dĺžka reťazca

$\color{purple}len\color{black}(cele)$

$\color{blue}14$

Zobrazenie časti reťazca r[n:m] Continue reading →

Python. Príloha 1. Zabudované funkcie

5.10.2017InformatikaPythonTibor Menyhért Leave a comment

Zabudované funkcie sú funkcie, ktoré sú v interpretri Python vždy k dispozícií, nemusíme ich importovať. Continue reading →

Python 2. Premenné a práca s reťazcami

5.10.2017InformatikaPythonTibor Menyhért Leave a comment

Aby program mohol zmysluplne pracovať, musíme ho „nakŕmiť“ informáciami, tieto informácie si program uloží do pamäti a potom s nimi pracuje. Pomenovaná časť pamäte sa nazýva premenná. Continue reading →

Slovníček termínov z informatiky

29.9.2017InformatikaTibor Menyhért Leave a comment

Ak tu nie je termín, ktorý som použil na hodinách informatiky alebo v niektorom článku, napíšte do komentára návrh na jeho doplnenie. Continue reading →

Hra Logik v Pythone

27.9.2017InformatikaTibor Menyhért Leave a comment

Pravidlá hry Logik:

Hráč 1 si myslí štvorciferné číslo bez opakovania číslic
Hráč 2 toto číslo háda tak, že povie štvorciferné číslo, bez opakovania číslic a hráč 1 odpovie koľko číslic je na správnom mieste a koľko číslíc do čísla patrí, ale nie sú na svojom mieste. Číslice na správnom mieste sú označené počtom A, číslice na nesprávnom mieste počtom B.

Continue reading →

Ako vyrobiť provizórnu náhradu kľúča

26.9.2017Informatika, Technická výchovaTibor Menyhért Leave a comment

V nasledujúcom videu je návod, ako možno vyrobiť náhradu kľúča s využitím mobilu, počítača, tlačiarne, vrhchnáka z plechovky a nožníc na železo. Continue reading →

Tabuľka ASCII

18.9.2017InformatikaTibor Menyhért Leave a comment

Informácie v počítači sú kódované podľa dohodnutých pravidiel. Najrozšírenejším kódovaním je kódovanie ASCII. Každý znak má pridelené nejaké číslo, napríklad A – 65, B – 66 až Z – 90.

Pôvodne malo kódovanie ASCII iba 128 znakovo od nula po 127, bolo to 7 bitové kódovanie, v súčasnosti je to 8 bitové kódovanie, takže možno zakódovať 256 znakov.

Ak sme v zahraničí, v internetovej kaviarni pravdepodobne nebude slovenská klávesnica. Znaky ako á, é, ô, ä … získame tak, že použijeme nasledujúcu tabuľku. Ak stlačíme a držíme stlačený kláves ALT a napíšeme číslice z tejto tabuľky a ALT pustíme, získame príslušný znak: Continue reading →

Kompresor obrázkov

8.6.2017InformatikaTibor Menyhért Leave a comment

Online komprimovanie obrázkov

Ak chcete zverejniť fotografie na www stránke, väčšinou stačí výrazne menšie rozlíšenie než má originálna fotografia a možno tiež použiť komprimovanie originálneho obrázku. Ak sú na stránke menšie obrázky, načíta sa výrazne rýchlejšie, zároveň na danom hostingu máte predplatený nejaký priestor a ak tam budete dávať zbytočne objemné súbory, tak si tento priestor veľmi rýchlo vyčerpáte. Zmenšenie rozlíšenia sa nijako neprejaví na kvalite obrázka, pokiaľ ho nebudete potrebovať zobraziť v pôvodnom rozlíšení. Dvojnásobné zmenšenie lineárnych rozmerov zmenší súbor štvornásobne, ak k tomu pridáte ešte komprimáciu, ktorá sa môže pohybovať okolo 70%, pôvodnú veľkosť súboru možno zmenšiť približne 12 násobne. Komprimácia obrázka môže jeho kvalitu znížiť, komprimačné algoritmy pre obrázky sú navrhnuté tak, aby napriek tomu, že ide o stratovú komprimáciu, ľudské oko nepostrehlo, že sa obrázok líši od originálu. Ak je zmena kvality zjavná, treba zmenšiť kompresný pomer.

Na tejto adrese nájdete jeden z online kompresorov obrázkov:

Compressjpeg.com

Pokiaľ potrebujete komprimovať obrázky pravidelne, je vhodnejšie mať na počítači nainštalovaný niektorý z programov, ktoré komprimáciu majú implementovanú.

Tic-Tac-Toe v Baltíku

25.5.2017InformatikaTibor Menyhért Leave a comment

Väčšina z vás sa na počítačoch najradšej hrá. Aj ja sa na počítačoch a mobiloch zvyknem hrať, ale najväčšou zábavou pre mňa je niečo naprogramovať. Kedysi som sa naučil programovať hlavne tým, že som programoval rôzne počítačové hry. Prvý počítač som si kúpil v roku 1985, bol to osembitový japonský počítač Sord, mal 8 kilobajtov pamäte a programy sa doň nahrávali pomocou kazetového magnetofónu. Do ôsmich KB sa toho veľa nezmestilo, preto som sa snažil programovať efektívne s čo najmenšími pamäťovými nárokmi a programujem tak doteraz. Vtedajšie počítače boli mnohotisíckrát pomalšie, ako dnešné, takže, ak hra mala byť hrateľná, bolo potrebné optimalizovať aj rýchlosť programu. Programovacím jazykom bol Basic a kritické časti som programoval v asemblery.

Na tento počítač takmer žiadne hry neexistovali a tak, keď som na iných počítačoch videl nejakú hru, naprogramoval som ju aj na mojom počítači.

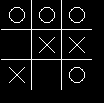Začneme jednoduchou logickou hrou Tic-Tac-Toe. Hrá sa na hracom pláne 3×3. Do plánu hráči striedavo zapisujú svoje symboly – krížik a krúžok. Kto uloží svoje symboly tak, že sú vedľa seba, pod sebou alebo po diagonále tri, vyhral. Ak sú všetky políčka obsadené a nik nemá tri rovnaké symboly v rade, hra skončila remízou. Na obrázku vpravo vyhral hráč, ktorý kreslil krúžky. Continue reading →

Projekt Sudoku

19.5.2017InformatikaSudokuTibor Menyhért Leave a comment

1. etapa

Na prvej hodine ste takmer všetci zvládli nakresliť hrací plán Sudoku (obrázok vpravo). Mnohí postupovali extenzívne, niektorí zvládli aj efektívnosť riešenia. Počet použitých príkazov sa pohyboval od 21 do 93 (mne sa to podarilo na 18 príkazov, svoje riešenie sprístupním, keď všetky triedy dokončia prvú etapu a sprístupním tiež najefektívnejšie riešenia žiakov a jedno či viac riešení, ktoré budú niečim originálne. Continue reading →

Súťaž v programovaní Imagine

17.5.2017InformatikaTibor Menyhért Leave a comment

Vašou úlohou je naprogramovať prázdny hrací plán hry Sudoku na čo najmenší počet príkazov. Riešenie musí byť vytvorením procedúry, ktorá tento hrací plán nakreslí a nemožno použiť už predkreslený obrázok.

Vzor, ako by mal hrací plán vyzerať:

Do počtu príkazov nepočítame viem názov_procedúry a koniec a číselné parametre či už vo forme čísla alebo premennej.

Celkové poradie

Čajka 9. A 18
Petróc 7.A 21
Micheĺ 9.A 22
Varinský 7.A 29
Richnavský 31

Poradie podľa jednotlivých tried

9.A

Čajka 18
Micheľ 22
Richnavský 31
Krajňáková 39
Sabovčíková a Genčiová 91
Kalina 98

7. A

Petróc 21
Varinský 29
Melicherová 31
Gbúrová 32
Lukáč, Orosz 75
Bucher 85

7. B

Sremaňák 40 (Patrikove riešenie zverejním, ako jediný použil parameter, ktorý určuje, aký veľký bude hrací plán)
Jakubčák 56
Šašala – veľa 🙂

Učiteľ TM 17. Pôvodne som mal 21, keď Petróc dosiahol rovnaký počet, ešte som to zredukoval.