Fyzika

Meranie tepelnej kapacity železnej kocky a hmotnostnej tepelnej kapacity železa

Fyzika, Leave a comment

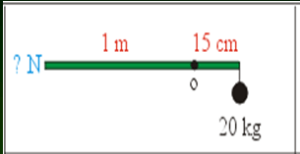
Pri meraní sme nevzali do úvahy tepelnú kapacitu kalorimetra. Toto meranie bolo realizované na hodine fyziky 7.B v roku 2024.

  • Prázdny kalorimeter sme položili na digitálnu váhu, stlačili sme tlačítko Tara
  • Do kalorimetra sme naliali studenú vodu a digitálna váha odmerala jej hmotnosť.
    m_1=129,6\, g=0,1296\, kg
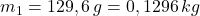
  • Do kalorimetra sme vložili teplomer, počkali sme, kým sa teplota ustáli.
    t_1=21,3\, ^oC
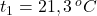
  • V rýchlovarnej kanvici sme zohriali vodu, do kadičky sme vložili železnú kocku a zaliali ju horúcou vodou. Po niekoľkých minútach sme odmerali teplotu vody v kadičke, túto teplotu sme pokladali za teplotu kocky.
    t_2=63,2\,^oC
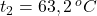
  • Kocku sme rýchlo vybrali z kadičky a vložili do kalorimetra.
  • Čakali sme, kým teplota vody v kalorimetri stúpala, keď prestala stúpať, zapísali sme dosiahnutú teplotu.
    t=24,8\,^oC
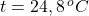
  • Vypočítali sme množstvo tepla, ktoré kocka odovzdala vode
    Q_1=c_1\cdot m_1 \cdot \Delta t_1
    Q_1=4180 \frac{ J}{ kg\cdot ^oC} \cdot 0,1296\, kg \cdot 3,5\,^oC
    Q_1=1896\, J
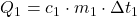
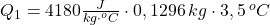
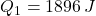
  • Množstvo prijatého a odovzdaného tepla je rovnaké.
    Q_1=Q_2
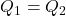
  • Odovzdané teplo možno vyjadriť ako súčin tepelnej kapacity kocky a rozdielu pôvodnej a konečnej teploty.
    Q_2=C \cdot \Delta t_2
    C= \cfrac{Q_1}{\Delta t_2}
    C= \cfrac{1896\, J}{63,2^oC-24,8^oC}
    C=49,38 \frac{J}{^oC}
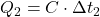
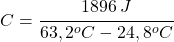
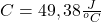
  • Hmotnostnú tepelnú kapacitu dostaneme ako podiel tepelnej kapacity telesa a jeho hmotnosti. Odvážili sme hmotnosť železnej kocky a vypočítali sme hmotnostnú tepelnú kapacitu železa.
    m_2=128,2\,g=0,1282 \,kg
    c=\cfrac{C}{m_2}
    c=\cfrac{49,38}{0,1282}=385\frac{ J}{ kg\cdot ^oC}
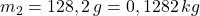
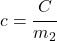
  • Vo fyzikálno-chemických tabuľkách sme vyhľadali hmotnostnú tepelnú kapacitu železa, jej hodnota je:
    c_{Fe}=450\frac{ J}{ kg\cdot ^oC}
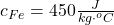
    Nami nameraná hodnota bola o 14,44% menšia než tabuľková.

Analýza prečo sme namerali menej, než je v tabuľkách?

  1. Nevzali sme do úvah tepelnú kapacitu kalorimetra. Kocka odovzdala teplo nielen vode, ale aj kalorimetru. Keď ju odmeriame, môžeme naše meranie upresniť.
  2. Vždy sa dopúšťame nejakej chyby merania, pri meraní teploty sme sa mohli pomýliť trikrát najmenej o pol desatiny stupňa, chyby sme sa mohli dopustiť aj pri meraní hmotnosti vody a kocky.
  3. Pri pokuse dochádzalo aj k tepelnej výmene s prostredím, pri prenose kocky do kalorimetra a hoci je kalorimeter zostrojený tak, aby sa minimalizovala tepelná výmena s okolím, predsa len k nejakej výmene dochádza.

Vzhľadom na vyššie uvedené je 14,44% chyba prijateľná.

Kalorimetrická rovnica

Fyzika, Leave a comment

Ak máme dve telesá, jedno teplejšie a druhé chladnejšie, ak sú tieto telesá v kontakte, dôjde k tepelnej výmene, teplejšie teleso odovzdá teplo chladnejšiemu a chladnejšie teleso príjme teplo od teplejšieho. Tepelná výmena trvá, až kým budú mať obe telesá rovnakú teplotu.

Ak prijaté teplo označíme Q_1 a odovzdané teplo Q_2 a telesá si nevymieňajú teplo s prostredím, platí kalorimetrická rovnica: Q_1=Q_2 . Množstvo prijatého tepla sa rovná množstvu odovzdaného tepla.

Continue reading →

Tepelná kapacita telesa

Fyzika, Matematika, Leave a comment

Tepelná kapacita telesa je množstvo tepla, ktoré je potrebné na zohriatie telesa o jeden stupeň celzia. Tepelnú kapacitu telesa označujeme veľkým C. Pri rôznych teplotách je tepelná kapacita telesa rôzna, ak rozdiel teplôt nie je veľký, môžeme tepelnú kapacitu telesa pokladať za konštantnú.

Množstvo tepla, ktoré teleso prijme alebo odovzdá pri tepelnej výmene závisí od jeho tepelnej kapacity a rozdielu teplôt \Delta t.

\Delta t=t_2-t_1, kde t_1 je pôvodná teplota telesa a t_2 je konečná teplota telesa.

Q=C\cdot\Delta t

Ak sa chceme vyhnúť záporným hodnotám tepla, môžeme v \Delta t na prvé miesto dať vyššiu teplotu.

Tepelná kapacita telesa rastie s jeho hmotnosťou. Koľkokrát je hmotnosť telesa z tej istej látky väčšia, toľkokrát je väčšia jeho tepelná kapacita. Na základe toho môžeme zaviesť termín hmotnostná tepelná kapacita.

Hmotnostná tepelná kapacita látky je množstvo tepla potrebné na zohriatie 1 kg látky o jeden stupeň celzia. Označujeme ju malým c. Hmotnostnú tepelnú kapacitu vypočítame zo vzorca:

c=\frac{ C}{m} kde m je hmotnosť telesa.

Hmotnostnú tepelnú kapacitu jednotlivých látok nájdeme v matematicko fyzikálno chemických tabuľkách. Môžeme ju tiež zistiť meraním a výpočtom z kalorimetrickej rovnice.

LátkaHmotnostná tepelná kapacita [c] \frac{ J}{ kg\cdot ^oC}
voda4180
hliník
meď
železo
olovo
ľad
vodík
dusík

Meranie objemu tuhých telies

Fyzika, Leave a comment

Objem tuhého telesa môžeme zistiť viacerými spôsobmi:

  • odmerným valcom
  • odmeraním rozmerov telesa a výpočtom
  • odmeraním hmotnosti telesa, použitím hustoty látky, z ktorej je teleso vyrobené a výpočtom

Meranie odmerným valcom

Do odmerného valca nalejeme kvapalinu, odmeriame jej objem, Objem kvapaliny označíme V_1. Potom do odmerného valca pridáme teleso, odmeriame objem kvapaliny s telesom, označíme ho V_2. Objem telesa určíme výpočtom V=V_2-V_1

Túto metódu môžeme použiť, len ak je teleso z látky, ktorá sa nepoškodí, ak sa ponorí do kvapaliny.

Odmeranie rozmerov telesa a výpočet

Ak má teleso taký tvar, pre ktorý je známy vzorec na výpočet objemu, odmeriame rozmery telesa a dosadíme ich do vzorca pre výpočet objemu.

Kocka

V=a^3

Stačí odmerať jednu hranu kocky.

Kváder

V=a.b.c

Odmeriame tri strany kvádra.

Guľa

V=\frac{4}{3}\pi r^3

Odmeriame priemer gule a predelíme ho dvoma.

Pomocou hustoty látky a hmotnosti

Zo vzorca pre výpočet hustoty vyplýva vzorec pre výpočet objemu, ak poznáme hustotu a hmotnosť:

V=\frac{m}{\rho}

Metódu môžeme použiť, len ak je teleso rovnorodé.

Časticové zloženie látok

Fyzika Leave a comment

Látky sú zložené z častíc – atómov a molekúl.

Atóm je základná častica látky. Jeho názov pochádza z gréčtiny zo slova atomos – nedeliteľný. Začiatkom 20. storočia vedci zistili, že aj atóm sa z čohosi skladá.

Molekula je častica, ktorá sa skladá z dvoch alebo viacerých atómov.

Na obrázku je molekula vody, ktorá sa skladá z dvoch molekúl vodíka a jednej molekuly kyslíka. Chemická značka H_2O.

Continue reading →

Látka a teleso

Fyzika Leave a comment

To čo v bežnom živote nazývame vec, predmet, výrobok, … vo fyzike nazývame teleso. Keď použijeme slovo teleso, budeme sa zaoberať jeho fyzikálnymi vlastnosťami.

Telesá môžu byť tvorené z rôznych látok: stolička môže byť z dreva, kovu, plastu, prípadne môže byť vyrobená z viacerých látok, každá časť je vyrobená z látky, ktorá najviac spĺňa požiadavky na ňu kladené. Vo fyzike to čo v bežnom živote nazývame materiál nazývame látka.

Telesá môžu byť z pevných, kvapalných alebo plynných látok, prípadne ich kombinácií.

Vedenie elektrického prúdu v kvapalinách

Fyzika Leave a comment

Keď do nádoby nalejeme destilovanú vodu (chemicky čistú vodu) a ponoríme do nej elektródy pripojené na zdroj elektrického napätia, obvodom nebude prechádzať elektrický prúd. Čiže chemicky čistá voda je nevodič.

Na hodine sme nemali k dispozícii destilovanú vodu, použil som vodu z vodovodu, kým bolo napätie nízke, obvodom elektrický prúd nepretekal . Keď som napätie zvýšil na cca. 8 voltov, zaznamenali sme prúd jedna stotina ampéra.

Continue reading →

Odpor žiarovky

Fyzika Leave a comment

Na hodine som previedol sadu meraní elektrického obvodu, v ktorom bola žiarovka. Postupne som zvyšoval napätie zdroja a meral prúd prechádzajúci obvodom. Namerané hodnoty iba čiastočne zodpovedali grafu, ktorý je v učebnici na strane 54. Samotné vodiče a merací prístroj totiž mali nejaký odpor, ktorý vzhľadom k odporu žiarovky nebol zanedbateľný. Po skončení hodiny som preto urobil druhú sadu meraní.

Continue reading →

Elektrická vodivosť

Fyzika, , Leave a comment

Meraním sme zistili, že elektrický odpor vodiča závisí od druhu materiálu, z ktorého je vodič vyrobený, od dĺžky vodiča a od plochy prierezu vodiča.

Najprv som meral elektrický prúd pre oceľový drôt s priemerom 0,2 mm pri konštantnom napätí, pre rôzne dlhé drôty. Zistili sme, že s rastúcou dĺžkou drôtu elektrický prúd klesá, teda elektrický odpor rastie.

Continue reading →

Geometrická optika

Fyzika Leave a comment

Geometrická optika alebo optika lúčov je oblasť fyziky, ktorá popisuje optické javy geometricky, zanedbávajúc vlnovú podstatu svetla.

Je založená na nasledujúcich princípoch:

  • princíp priamočiareho šírenia svetla
  • princíp vzájomnej nezávislosti lúčov
  • princíp zameniteľnosti chodu lúčov
  • zákon odrazu
  • zákon lomu

Princíp priamočiareho šírenia svetla

Svetlo sa v homogénnom (rovnorodom) prostredí šíri priamočiaro.
Ak máme veľmi malý zdroj svetla (bodový zdroj svetla) uzavretý v nepriehľadnej schránke, na ktorej je kruhový otvor, svetlo uniká iba týmto otvorom a vytvára svetelný kužeľ, ako je na obrázku hore, tento svetelný kužeľ môžeme vidieť, pokiaľ sú vo vzduchu drobné prachové častice. Ak do kužeľa vložíme tienidlo, kolmo na os kužeľa, zobrazí sa na tienidle kruh, ten je tým väčší, čím sme ďalej od zdroja svetla a čím je otvor na schránke väčší.

Princíp nezávislosti lúčov

Svetelné lúče prechádzajú prostredím tak, akoby ostatné lúče neexistovali.

Princíp zámeny chodu lúčov

Ak sa svetelný lúč šíri z bodu A do bodu B, potom sa môže šíriť z bodu B do bodu A a to po tej istej dráhe.

Zákon odrazu

Uhol odrazu sa rovná uhlu dopadu.

Zákon lomu

Keď svetelný lúč prechádza z jedného prostredia do druhého, tak sa lúč zlomí podľa nasledujúceho vzťahu:
\dfrac{sin, \alpha _1}{sin, \alpha_2}=\dfrac{sin, v_1}{v_2}=\dfrac{n _2}{n_1}

Kde \alpha _1 je uhol dopadu, \alpha _2 je uhol lomu, v_1 je rýchlosť svetla v prvom prostredí, v_2 rýchlosť svetla v druhom prostredí a n_1, n_2 sú relatívne indexy lomu prvého a druhého prostredia.

Znamienková konvencia

  • Predmetová vzdialenosť je kladná pred šošovkou, záporná za šošovkou.

Šošovky

Fyzika Leave a comment

Šošovka je homogénne izotropné prostredie, ohraničené dvoma guľovými plochami alebo guľovou plochou a rovinou. Je to predmet z priehľadného materiálu slúžiaci v optike alebo v iných prípadoch na ovplyvnenie šírenia svetla v širšom zmysle, t. j. viditeľného svetla, infračerveného a ultrafialového žiarenia.

Šošovky sú najčastejšie sklenené, ale na ich výrobu sa bežne používajú aj plasty. Materiál šošovky je charakterizovaný indexom lomu, ktorý je vždy väčší ako jedna, a indexom absorpcie, ktorý je pre vlnové dĺžky v rozsahu použiteľnosti šošovky blízky nule. Najjednoduchší opis šírenia lúčov šošovkou poskytuje geometrická optika. Ak je hrúbka šošovky vzhľadom na polomery jej guľových plôch zanedbateľná (d<<r), potom hovoríme, že šošovka je tenká.

Najstaršia zmienka o šošovke pochádza z Aristofanovej divadelnej hry Oblaky, kde vystupovala ako zapaľovacie sklíčko.

Druhy šošoviek

Základné delenie šošoviek vychádza z toho, či šošovka rovnobežné lúče spája alebo rozptyľuje.

  • spojky – lúče spájajú
  • rozptylky – lúče rozptyľujú

Na obrázku v pravo sú rôzne tvary šošoviek. Šošovky 1 až 3 sú spojky, 4 až 5 rozptylky.

Spojka (spojná šošovka, konvexná šošovka)

Spojka je uprostred hrubšia ako na okrajoch a má aspoň jeden vypuklý povrch. Na obrázku v pravo je ukážka, ako prechádzajú vodorovné lúče šošovkou.

Zdroje:

  • Časť textu je prevzatá zo slovenskej wikipédie
  • Obrázky sú prevzaté z wikipédie

Teplo a teplota

Fyzika, Leave a comment

V bežnom živote často nerozlišujeme medzi teplom a teplotou. Ak povieš „Je mi teplo.„, ide čiastočne o subjektívny pocit, vedľa sediacemu kamarátovi môže byť zima. Ak povieme vonku je teplo, myslíme tým, že je vonku vysoká teplota.

Vo fyzike striktne rozlišujeme medzi teplom a teplotou.

Teplota je fyzikálna veličina, ktorá súvisí s vnútornou energiou látky.

Dve telesá majú rovnakú teplotu, ak priemerná kinetická energia ich častíc je rovnaká. O teplote má zmysel hovoriť len u makroskopických telies. Hovoriť o teplote jednotlivej častice nemá zmysel.

Základnou jednotkou teploty je Kelvin, značka K. Vedľajšou jednotkou je stupeň celzia, značka ^0C. V bežnom živote používame stupne celzia.

Continue reading →

Elektrický prúd

Fyzika Leave a comment

Elektrický prúd je fyzikálna veličina. Je to usporiadaný pohyb elektrického náboja.

Značka elektrického prúdu je I.

Jednotkou elektrického prúdu je ampér, značka A.

Ak vodičom prechádza elektrický prúd jeden ampér, preteká ním náboj jeden coulomb za sekundu.

1A = 1C/s

Voľné elektróny vytvárajú v kovovom vodiči elektrický oblak. Voľné elektróny sa vo vodiči pohybujú chaoticky všetkými smermi. Hoci sa elektrický náboj pohybuje, zo štatistického hľadiska sa rovnaké množstvo elektrického náboja pohybuje jedným i druhým smerom a teda nejde o usporiadaný pohyb elektrónov a nejedná sa o elektrický prúd.

Ak konce vodiča pripojíme k zdroju elektrického napätia, elektróny sa začnú pohybovať ku kladnému pólu zdroja. Naďalej budú vykonávať aj chaotický tepelný pohyb, ale vo vodiči bude aj usporiadaná zložka tohto pohybu. Vznikne usporiadaný pohyb elektrického náboja, ktorý nazývame elektrický prúd. Na elektróny pôsobí príťažlivá sila, pohybujú sa zrýchlene, ale často narazia do atómov vodiča a ich pohyb sa spomalí. Vodičom bude prechádzať prúd stálej veľkosti.

Základné pojmy z optiky a základné vlastnosti svetla

Fyzika Leave a comment
Skladanie farieb cez farebné filtre

Viditeľné svetlo alebo len svetlo je elektromagnetické vlnenie s vlnovou dĺžkou približne 390 nm až 760 nm (nanometer je jedna miliardtina metra). Vnímame ho zrakom, pričom farba závisí od vlnovej dĺžky svetla (červená farba má najväčšiu a modrá najmenšiu vlnovú). Viditeľné svetlo tvorí 48% slnečného žiarenia. 

Oblasť fyziky, ktorá sa zaoberá viditeľným svetlom, sa nazýva optika.

Continue reading →

Zákon sily

Fyzika Leave a comment

Zo skúsenosti vieme, že:

  • oveľa ľahšie roztlačíme vozík s malým dieťaťom než rovnaký vozík s ťažkým chlapom
  • ak sa rovnakou rýchlosťou pohybuje vozík s malým dieťaťom a s ťažkým chlapom, vozīk s dieťaťom zastavīme výrazne ľahšie

Pokus: K prázdnemu a naloženému vozíku priviažeme špagáty, tie vedieme cez kladky a na druhý koniec špagátov priviažeme rovnaké závažia. Prázdny vozík bude mať väčšie zrýchlenie než plný, pričom na oba vozíky pôsobila rovnaká sila.

Na základe podobných pokusov môžeme odvodiť zákon sily.

Zákon sily (2. Newtonov pohybový zákon): Zrýchlenie telesa v inerciálnej vzťažnej sústave je priamo úmernė sile, ktorá naň pôsobī a nepriamo úmerné hmotnosti telesa.

Continue reading →

Zákon zotrvačnosti

Fyzika Leave a comment

Každodenne sa stretåvame s takýmito a podobnými javmi:

  • ak cestujeme mestskou hromadnou dopravou a šofér prudko akceleruje, ak sa nedržíme, môžeme spadnúť, zdá sa nám, akoby na nás pôsobila sila, pôsobiaca v opačnom smere, než je smer pohybu vozidla
  • ak vodič prudko zabrzdí, naopak nás nejaká sila „hodí“ dopredu
  • ak vodič prechádza rýchlo zákrutou, nejaká sila nás tlačí nabok
  • keď sa v pračke začne bubon otáčať vo vysokých obrátkach, prádlo sa vyžmýka

Všetký tieto javy sú dôsledkom zákona zotrvačnosti.

Zákon zotrvačnosti (1. Newtonov pohybový zákon): Teleso v inerciálnej sústave zotrváva v pokoji alebo v rovnomernom priamočiarom pohybe, ak výslednica síl naň pôsobiacich je nulová.

Continue reading →

Newtonove pohybové zákony

Fyzika Leave a comment
Isaac Newton (1643-1727)

Newtonove pohybové zákony alebo Newtonove zákony pohybu alebo Newtonove princípy sú základné zákony mechaniky, ktoré zverejnil Isaac Newton v diele Philosophiae naturalis principia mathematica v r. 1687. Tvoria axiomatický základ Newtonovej mechaniky.

Sú to tieto tri zákony:

Zobraziť článok

  1. Newtonov pohybový zákon (zákon zotrvačnosti): Teleso v inerciálnej sústave zotrváva v pokoji alebo v rovnomernom priamočiarom pohybe, ak výslednica síl, ktoré naň pôsobia je nulová.
  2. Newtonov pohybový zákon (zákon sily): Zmena hybnosti telesa za jednotku času je priamo úmerná veľkosti pôsobiacej sily.
  3. Newtonov pohybový zákon (zákon akcie a reakcie): Ak jedno teleso pôsobí na druhé teleso nejakou silou, druhé teleso pôsobí na prvé teleso rovnako veľkou silou opačného smeru.

Newtonove pohybové zákony umožňujú určiť, aký bude pohyb telesa v inerciálnej vzťažnej sústave, ak sú známe všetky sily, ktoré naň pôsobia.

Podrobnejšie v jednotlivých článkoch o pohybových zákonoch.

Zdroje:

Kmitavý pohyb

Fyzika Leave a comment

Kmitavý pohyb je pohyb, ktorý sa pravidelne opakuje.

Zariadenia vykonávajúce pravidelne sa opakujúci pohyb:

a) kyvadlo
b) teleso zavesené na pružine
c) tyč upevnená na jednom konci
d) kvapalina v trubici v tvare U
e) hodinový nepokoj
f) struna

Kyvadlo. Rýchlosť, zrýchlenie, uhol výchylky
Pružina

Kmitavý pohyb môže byť:

a) priamočiary
b) krivočiary
c) otáčavý
d) nerovnomerný (nerovnomerný je vždy)

Kmit: periodicky sa opakujúca sa časť kmitavého pohybu

Doba kmitu (perióda): doba, za ktorú sa vykoná jeden kmit. Značka: T

Frekvencia (kmitočet): Počet kmitov za sekundu. Značka: f

Metóda Monte Carlo

Fyzika, Informatika Leave a comment

Náhoda hrá vo vede významnú úlohu. Mnohé dôležité objavy boli objavené na základe náhodných okolností. Niektoré sú možno iba mytologizáciou skutočnosti napríklad objav Archimedovho zákona a údajný beh nahého Archimeda Syrakúzami vykrikujúceho Heuréka! alebo Pád jablka na hlavu Newtona. Mnohé iné sa určite stali napríklad Flemingov objav penicilínu. Vo všetkých týchto prípadoch však popri náhode bolo dôležité, že príslušný vedec mal adekvátne vedomosti a tvorivú myseľ a tak hoci predtým tisíckam ľudí padli jablká či hrušky na hlavu, až Newton si dal veci do súvisu a prišiel na to, že rovnaká sila udržiava planéty okolo Slnka a Mesiac okolo Zeme, aká pôsobí na padajúce jablko, stovky vedcov mali neumyté misky a iba ich umyli, pričom si nevšimli žiadnu anomáliu až Fleming aj pri umývaní misiek premýšľal. Keď môže byť náhoda alebo omyl čas od času príčinou pokroku, stojí za úvahu, či neskúmať niektoré prírodné javy pomocou využitia náhody. Continue reading →

Správanie sa telies v kvapalinách

Fyzika Leave a comment

Zo skúsenosti viete, že keď sa nachádza tuhé teleso v kvapaline, tak v nej buď pláva alebo sa potopí. Na hodine sme spravili nasledujúci pokus:

Do nádoby s vodou sme vložili prázdnu rozrezanú krabičku od džúsu. Miska vo vode plávala, Keď sme do nej vložili hlíníkové závažie, naďalej plávala. Keď sme hliníkové závažie zamenili železným závažím rovnakých rozmerov, krabička sa potopila, Z toho sme usúdili, že či teleso bude alebo nebude plávať nejako závisí od hmotnosti telesa.

Keď sme nahradili malú krabičku veľkou krabicou, krabica plávala aj so železným závažím. Z toho sme usúdili, že či teleso bude alebo nebude plávať nejako závisí od objemu telesa.

Continue reading →

Riešené príklady na výkon a prácu

Fyzika Leave a comment

Pri počítaní príkladov na výkon využijeme všetky vzorce, ktoré sme preberali v súvislosti s prácou, silou, trením, gravitačnou silou, …  Základné vzorce:

  • gravitačná sila F_g=m.g
  • gravitačné zrýchlenie g=10\cfrac{N}{kg}
  • statické trenie F=f_0.F_N, kde F_N je sila pôsobiaca kolmo na podložku, f_0 je koeficient statického trenia
  • dynamické trenie F=f.F_N, kde f je koeficient dynamického trenia
  • mechanická práca W=F.s, ak sila a smer pohybu sú rovnobežné, inak silu musíme rozložiť na zložku pôsobiacu v smere pohybu a na zložku kolmú na tento pohyb.
  • výkon P=\cfrac{W}{t}

Continue reading →

Ohmov zákon. Elektrický odpor

Fyzika Leave a comment

Video, kde som odmeral závislosť elektrického prúdu od elektrického napätia pri dvoch rôznych rezistoroch (rovnaký pokus s inými rezistormi budete robiť, keď sa vrátite do školy).

Tabuľka nameraných hodnôt z videa
Schéma zapojenia obvodu v meraní z videa
(voltmeter bol zabudovaný priamo v zdroji)
Graf závislosti I od U. Modro sú namerané hodnoty, červene je graf pre priemerný odpor.
Ak tam tá červená čiara nie je, tak voľným okom takmer nevidíme, že modrá čiara nie je priamka.

Georg Ohm

Georg Ohm experimentálne zistil, že pre kovové vodiče platí  priama úmernosť veľkosti elektrického prúdu od  veľkosti napätia (ak je teplota vodiča stála).

Ohmov zákon: Elektrický prúd pretekajúci v uzavretom elektrickom obvode je priamo úmerný napätiu zdroja a nepriamo úmerný elektrickému odporu obvodu.

I=\cfrac{U}{R} \,(1)

Elektrický odpor je fyzikálna veličina. Značka R. Je to podiel elektrického napätia a elektrického prúdu.  R=\cfrac{U}{I} \,(2).

Jednotkou odporu je ohm, značka \Omega.

1\,\Omega=\cfrac{1\, V}{1\, A}\,(3) Continue reading →

Výkon

Fyzika Leave a comment

Na vykonávanie mechanickej práce ľudia v minulosti používali rôzne zvieratá: voly, kone, osly, slony, … Využívali aj energiou vetra (veterné mlyny, plachetnice) alebo energiu vody ( vodné mlyny, hámre, …).

Už v prvom storočí nášho letopočtu zostrojil prvý parný stroj Herón Alexandrijský, ale bol používaný skôr pre zábavu, než na vykonávanie užitočnej práce. Parný stroj opäť vynašiel Thomas Newcomen v roku 1712. Výrazne ho zdokonalil James Watt, takže mnohí pripisovali vynález parného stroja Wattovi. Continue reading →

Elektrický prúd v kovovom vodiči. Tepelné účinky prúdu

Fyzika, , Leave a comment

Z chémie viete, že všetky prvky sa skladajú z atómov a jednotlivé atómy sa skladajú z protónov, elektrónov a neutrónov. Protóny majú kladný elektrický náboj, elektróny záporný elektricky náboj a neutróny elektrický náboj nemajú – preto sa volajú neutróny, lebo sú elektricky neutrálne. Atóm je elektricky neutrálny, má rovnaký počet elektrónov a protónov. V kovoch sa elektróny, ktoré sú vo vonkajšej  vrstve elektrónového obalu, chovajú tak, akoby nepatrili ku konkrétnemu atómu, ale ku všetkým atómom v ich okolí. Hovoríme im voľné elektróny. Keď na konce kovového vodiča pripojíme zdroj elektrickej energie, tieto voľné elektróny sa začnú pohybovať smerom ku kladnému pólu zdroja. Continue reading →

Jednoduchý elektrický obvod

Fyzika Leave a comment

Jednoduchý elektrický obvod môžeme vytvoriť zo zdroja elektrickej energie, napr. batérie a spotrebiča, napr. žiarovky. Elektrickým obvodom prechádza elektrický prúd, ak je obvod uzavretý a je v ňom zapojený zdroj elektrickej energie. Aby elektrickým obvodom prechádzal elektrický prúd, musia byť všetky jeho časti vodivé.

Látky, ktoré vedú elektrický prúd, nazývame elektrické vodiče.

Látky, ktoré nevedú elektrický prúd, nazývame nevodiče alebo elektrické izolanty.

Látky, ktoré za istých okolností vedú elektrický prúd a za iných okolností elektrický prúd nevedú nazývame polovodiče.

Continue reading →

Valivé trenie

Fyzika One Comment

Zo skúsenosti vieme, že ak máme teleso v tvare valca, musíme vynaložiť oveľa menšiu silu, keď ho kotúľame po plášti, než keď ho tlačíme alebo ťaháme po základni. Ak na premiestnenie po tej istej dráhe vynaložíme väčšiu silu, vykonáme väčšiu prácu a teda minieme viac energie.  Preto sa snažíme čo najviac minimalizovať trenie. Ušetríme tým vynaloženú prácu a v dôsledku toho, znížime náklady na rovnaký výsledný efekt. Continue reading →

Trenie

Fyzika One Comment

Vykonali sme niekoľko pokusov, pri ktorých sme skúmali, aká minimálna sila musí pôsobiť na teleso ležiace na vodorovnej podložke, aby sa pohlo a aká sila naň musí pôsobiť, ak je v pohybe, aby sa pohybovalo rovnomerne priamočiaro.

Zistili sme:

  1. Veľkosť prvej sily je väčšia než druhej
  2. Veľkosť oboch síl  závisí od materiálov podložky a trecej plochy telesa. Kváder, ktorý mal steny z troch povrchov ( drevo, koža a oceľ) sa po laboratórnom stole najľahšie pohyboval na oceľovej strane a najťažšie na koženej strane.
  3. Koľkokrát sa zväčší hmotnosť telesa, toľkokrát sa zväčší sila, ktorá musí pôsobiť, aby sa teleso pohlo, alebo, ak je v pohybe, konalo rovnomerný priamočiary pohyb..
  4. Trecia sila nezávisí od veľkosti trecej plochy (pokiaľ tlak nie je priveľký a nie sú prekročené medze pevnosti materiálu, text vyznačený kurzívou sme nedokázali, je to moje, zatiaľ pokusom nepotvrdené tvrdenie a v literatúre sa o tejto samozrejmosti (?) obvykle nepíše).
  5. Toto sme nezistili, ale pokusmi by sme zistiť mohli: Sila šmykového trenia pre malé rýchlosti, nezávisí od rýchlosti, ktorou sa teleso pohybuje.

Sila, ktorú sme merali, nazývame trecia sila a tento fyzikálny jav nazývame trenie. Trenie v pokoji je pokojové trenie, trenie v pohybe je šmykové trenie. Continue reading →

Vitálna kapacita pľúc

Fyzika, Leave a comment

Doma ste vyrobili spirometer – prístroj na meranie vitálnej kapacity pľúc.

Použili ste fľašu na zaváranie, vrchnák, dve slamky a izolačný materiál napríklad plastelínu alebo lepidlo. Do vrchnáku ste urobili dve dierky, cez ktoré ste prestrčili slamky. Diery okolo slamiek ste zaizolovali a zafixovali. Jedna zo slamiek bola zastrčená tak, aby dosahovala takmer na dno, druhá bola väčšmi vysunutá von, aby sme do nej mohli fúkať vzduch. Continue reading →

Využitie vlastností plynov

Fyzika Leave a comment

Prezentácia v PDF

Vlastnosti plynov

Rôznymi jednoduchými pokusmi sme si dokázali, že plyny majú nasledujúce vlastnosti:

  • tečú, sú tekuté (aj kvapaliny sú tekuté, preto plyny a kvapaliny nazývame tekutiny)
  • dajú sa ľahko rodeliť
  • nemajú stály tvar, majú tvar nádoby, v ktorej sa nachádzajú, vždy vyplnia celý objem nádoby
  • ľahko sa dostanú na ťažko dostupné miesta
  • sú stlačiteľné, nemajú stály objem
  • rozpínajú sa

Pascalov zákon

Pascalov zákon platí aj pre plyny.

Ak zatlačíme na plyn v uzavretej nádobe, zväčší sa všade vnútri v plyne tlak rovnako vo všetkých smeroch.

Všetky vyššie uvedené vlastnosti vieme využiť v rôznych zariadeniach a výrobkoch. Continue reading →

Elektrické vlastnosti látok. Elektrický náboj

Fyzika, One Comment

Pri obliekaní či vyzliekaní svetra ste neraz pozorovali, že sa vám zelektrizovali vlasy, niekedy sa vám to stane aj pri česaní – vlasy sú priťahované ku hrebeňu. Keď sú vlasy vlhké, zelektrizovanie nepozorujeme.

Zelektrizovanie telies možno dosiahnuť viacerými spôsobmi. Príčina zelektrizovania je v štruktúre látky. 

Podobne, ako magnetické vlastnosti dokážeme využiť aj elektrické vlastnosti látok. Continue reading →

Fyzikálna veličina

Fyzika 3 komentáre

Fyzikálna veličina je vlastnosť fyzikálneho objektu alebo fyzikálneho javu, ktorú možno merať.

Aby sme s fyzikálnymi veličinami vedeli počítať a odvodzovať medzi nimi vzťahy a fyzikálne zákony, každá fyzikálna veličina má svoju značku.

Fyzikálne veličiny meriame vo fyzikálnych jednotkách. Napríklad dĺžku v metroch, objem v litroch alebo metroch kubických, hmotnosť v kilogramoch, rýchlosť v metroch za sekundu, … Aj fyzikálne jednotky majú svoje značky.

Mnohé fyzikálne jednotky sú pomenované na počesť vedcov, ktorí sa zaoberali skúmaním javov, ktoré fyzikálna veličina spojená s jednotkou popisuje (sila newton, tlak pascal, elektrický prúd ampér, …).

Zoznam fyzikálnych veličín s ktorými sa oboznámite na základnej škole.