Funkcia na množine D je ľubovoľný predpis, ktorý každému prvku množiny D priradí práve jedno reálne číslo. Funkciu označujeme malým písmenom.

Prvky množiny D nazývame nezávislá premenná, ich obrazy sú závislá premenná. Nezávislú premennú obvykle označujeme x a závislú y, ale môžeme zvoliť také označenie, aby bolo zrejmé čo tieto premenné označujú. napríklad , kde je dráha, je konštantná alebo priemerná rýchlosť a je čas.

Continue reading →

Z mnohočlenmi môžeme robiť rovnaké operácie ako s číslami. Majme dva mnohočleny:

• sčítanie:
• odčítanie:
• násobenie:
• delenie:

Continue reading →

Mnohočlen alebo polynóm n-tého stupňa je algebraický výraz v tvare:

kde sú číselné konštanty a je premenná. Exponenty pri premennej sú prirodzené čísla, konštanty sú reálne čísla a .

Poznámka: termín polynóm pochádza z gréčtiny, kde poly je mnoho a nóm je člen.

Polynóm je napríklad: alebo

Polynóm môže obsahovať aj viacero premenným napríklad:

Continue reading →

Algebraický výraz je zápis skladajúci sa z čísel a z písmen (tie označujú premenné), ktoré sú pospájané znakmi matematických operácií, ako sú napríklad sčítanie, odčítanie, násobenie, delenie, umocnenie, odmocnenie, goniometrické funkcie, logaritmy, absolútna hodnota, atď. Môžu obsahovať aj zátvorky, ktoré určujú poradie (prioritu) vykonávania naznačených operácií. Výrazy sú napríklad zápisy:

Ak namiesto premenných zadáme konkrétne číselné hodnoty, dostaneme hodnotu algebraického výrazu.

Continue reading →

Mocninová funkcia je funkcia v tvare:

Continue reading →

Odmocňovanie je opačná operácia k umocňovaniu. .

Opačnou operáciu k sčítaniu je odčítanie a zistili sme, že odčítanie sa dá previesť na sčítanie. K číslu pripočítame záporné číslo:

Podobne delenie je opačnou operáciu k násobeniu a zistili sme, že delenie sa dá previesť na násobenie:

Analogicky by mohlo platiť, že by sme nejako mohli previesť odmocňovanie na umocňovanie.

Continue reading →

Druhá odmocnina z a je také číslo b pre ktoré platí:

označujeme ho

Odmocňovanie je opačná operácia k umocňovaniu, takže platí:

Podobne možno zadefinovať tretiu odmocninu:

Tretia odmocnina z a je také číslo b pre ktoré platí:

označujeme ho

Všeobecne: n-tá odmocnina z a je také číslo b pre ktoré platí:

označujeme ho

Platí:

Continue reading →

Mocniny čísla 10:

Počítame v desiatkovej sústave. Čislo 3456 možno zapísať v tvare:

Čísla 1, 10, 100, 1000 sú mocniny čísla 10, takže toto číslo môžeme zapísať aj v tvare:

Podobne aj desatinné čísla môžeme zapísať ako súčet mocnín čísla desať:

Niekedy spracujeme s veľmi veľkými alebo s veľmi malými číslami. Často je pohodlnejšie takéto čísla zapísať v tvare súčinu nejakého čísla a mocniny desiatky. Napríklad číslo: 1 235 000 000 – jedna miliarda 235 miliónov možno zapísať takto:

Alebo číslo

Continue reading →

Už na základnej škole ste sa stretli s druhou a treťou mocninou a so zovšeobecnením pre umocňovanie na ľubovolné prirodzené číslo.

Druhá mocnina:

Druhu mocninu ste používali napríklad pri výpočte obsahu štvorca a kruhu a pri Pytagorovej vete.

Obsah štvorca so stranou :

Obsah kruhu s polomerom :

Pytagorova veta:

Tretia mocnina:

Tretiu mocninu ste používali napríklad pri výpočte objemu kocky a objemu gule.

Objem kocky so stranou :

Objem gule s polomerom :

n-tá mocnina

Zovšeobecnením môžeme zaviesť mocninu na n:

Súčin n rovnakých činiteľov nazývame n-tá mocnina.

Pravidlá pre počítanie s mocninami

Možno dokázať nasledujúce pravidlá pre počítanie s mocninami:

Dôkazy nájdete v tomto článku (zatiaľ nenapísané)

Príklady:

Vzorec:

Čo je prvá mocnina?

Použili sme vzorec pre delenie mocnín s rovnakým základom a skutočnosť, že v čitateľovi sa nachádza o jeden raz častejšie než v menovateľovi, takže po vykrátení nám zostane len .

Čo je nultá mocnina?

Znova sme použili vzorec a skutočnnosť, že podiel dvoch rovnakých čísel je 1.

Čo sú záporne celé mocniny?

Príklady:

Prirodzené čísla: Čísla, ktoré označujú počet alebo poradie nazývame prirodzené čísla. Množinu prirodzených čísel označujeme písmenom N.

Podľa tejto definície je aj nula prirodzené číslo, niektoré matematické kurzy nulu za prirodzené číslo nepovažujú.

kde .

Čísla označujúce poradie sa tiež nazývajú ordinálne čísla (z angl. order).
Čísla označujúce počet prvkov množiny, respektíve veľkosť množiny sa tiež nazývajú kardinálne čísla.

Súčet dvoch prirodzených čísel je prirodzené číslo. Množina prirodzených čísel je vzhľadom na operáciu sčítania uzavretá.

Množina prirodzených čísel nie je vzhľadom na operáciu odčítania uzavretá. Napríklad 2-3 nie je prirodzené číslo. Ak chceme zadefinovať množinu, ktorá je vzhľadom na operáciu odčítania uzavretá, dospejeme k pojmu množina celých čísel.

Celé čísla: Celé čísla sú zjednotením množiny prirodzených čísel a čísel k nim opačných. Opačné číslo k číslu a je -a. K -a dospejeme aj takto 0-a=-a. Súčet opačných čísel je nula. Množinu celých čísel označujeme písmenom Z.

Množina celých čísel je uzavretá vzhľadom na operácie: sčítanie, odčítanie a násobenie. Ak chceme, aby sme dostali množinu, ktorá je uzavretá aj na operáciu delenie, dospejeme k množine racionálnych čísel.

Racionálne čísla: Racionálne čísla sú čísla, ktoré možno vyjadriť v tvare zlomku:

kde .

Racionálne čísla označujeme písmenom Q.

Množina racionálnych čísel je uzavretá vzhľadom na operácie: sčítanie, odčítanie, násobenie a delenie s výnimkou delenia nulou. Ak si zavedieme operácie umocňovanie a k nej opačnú (inverznú operáciu) odmocňovanie, tak zistíme, že množina racionálnych čísel znova nie je uzavretá vzhľadom na operáciu odmocňovanie. Keď však zostrojíme štvorec so stranou 1, tak vidíme, že existuje úsečka, ktorá má dĺžku . je to uhlopriečka tohto štvorca. Možno pritom dokázať, že nemožno vyjadriť v tvare zlomku. Takto dospejeme k pojmu množina reálnych čísel.

Reálne čísla: Reálne čísla sú čísla, ktoré možno zobraziť na číselnej osi. Reálne čísla sú dĺžky všetkých úsečiek. Reálne čísla označujeme písmenom R.

Iracionálne čísla: Reálne čísla, ktoré nie sú racionálne nazývame iracionálne čísla. Nedajú sa vyjadriť v tvare zlomku dvoch celých čísel.

Pre horeuvedené číselné množiny platí:

Slovom N je podmnožinou Z, Z je podmnožinou Q a Q je podmnožinou R.

Množina je súbor objektov o ktorých vieme rozhodnúť, či do množiny patria.
Množiny obvykle označujeme veľkými písmenami.

Prvok množiny: Objekt, ktorý do množiny patrí, nazývame prvok množiny.

Prvky množiny obvykle označujeme malými písmenami.

Výraz čítame ako p je prvkom A.

Výraz čítame ako p nie je prvkom A.

Podmnožina: Ak pre každý prvok množiny A platí, že je prvkom množiny B množina A je podmnožinou B

Výraz čítame ako A je podmnožinou B.

Vlastná podmnožina: Ak existuje aspoň jeden prvok množiny B, ktorý nie je prvkom A a A je podmnožinou B, potom A je vlastnou podmnožinou B.

Značíme výrazom:

Grafické vyjadrenie podmnožiny

Príklady množín a ich podmnožín:

• množina cicavcov je podmnožinou množiny zvierat
• množina zvierat je podmnožinou množiny živočíchov
• množnina párnych čísel je podmnožinou celých čísel
• množina dravcov nie je podmnožinou množiny cicavcov – existujú aj dravé vtáky a dravé ryby
• množina žiakov triedy je podmnožinou žiakov školy

Nadmnožina: Ak množina A obsahuje všetky prvky množiny B, množinu A nazývame nadmnožina množiny B.

Prázdna množina: Množina, ktorá nemá prvky sa nazýva prázdna množina.

Značíme buď { } alebo

Množinu môžeme určiť troma spôsobmi:

• vymenovaním prvkov
• uvedením vlastností, ktoré majú prvky spĺňať
• množinovými operáciami

a kombináciou hore uvedených spôsobov.

Operácie s množinami

Zjednotenie množín: Zjednotením množiny A a množiny B je množina všetkých prvkov, ktoré sú prvkami množiny A alebo množiny B.

Značíme:

Zjednotenie množín môžeme zapísať v tvare

Poznámka: je logická spojka alebo.

Graficky možno zjednotenie vyjadriť pomocou Vennovho diagramu:

Prienik množín: Prienikom množiny A a množiny B je množina všetkých prvkov, ktoré sú prvkami množiny A a množiny B.

Značíme:

Prienik množín môžeme zapísať v tvare:

Poznámnka: je logická spojka a.

Grafické vyjadrenie prieniku množín Vennovym diagramom

Rozdiel množín: Rozdiel množín A a B je množina všetkých prvkov, ktoré patria do A a nepatria do B.

Vennov diagram rozdielu množín

Zdroje

Obrázky sú prevzaté z wikipédie.

https://sk.wikipedia.org/wiki/Rozdiel_mno%C5%BE%C3%ADn

https://sk.wikipedia.org/wiki/Prienik_(matematika)

https://sk.wikipedia.org/wiki/Zjednotenie_(matematika)

V živote sa často stretávame so situáciou, keď je celok rozdelený na niekoľko rovnakých častí. Napríklad pizza, čokoláda, bomboniera s rovnakými cukríkmi, …

Matematika by mala poskytovať aparát, ktorý umožňuje počítať s takýmito časťami celku. Časť celku, či viacero rovnakých častí celku nazývame zlomok.

Zlomok je číslo v tvare

je množina celých čísel, je znak patrí do množiny. Vyššie uvedený výraz možno prečítať sú celé čísla a sa nerovná nula.

Číslo nad zlomkovou čiarou nazývame čitateľ, číslo pod zlomkovou čiarou nazývame menovateľ, čiara medzi čitateľom a menovateľom je zlomková čiara.

Krátenie zlomku

Ak čitateľa i menovateľa predelíme tým istým číslom rôznym od nuly, hodnota zlomku sa nezmení. Nazývame to krátenie zlomku. Napríklad:

Rozšírenie zlomku

Ak čítateľa i menovateľa vynásobíme tým istým číslom rôznym od nuly, hodnota zlomku sa nezmení. Nazývame to rozšírenie zlomku. Npríklad: \dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\dfrac{a}{b}+\dfrac{c}{d}= \dfrac{a\cdot d}{b \cdot d} +\dfrac{c\cdot b}{d\cdot b}=\dfrac{a \cdot d+c \cdot b}{b \cdot d}\dfrac{a}{c}-\dfrac{b}{c}=\dfrac{a-b}{c}\dfrac{a}{b}-\dfrac{c}{d}= \dfrac{a\cdot d}{b \cdot d} -\dfrac{c\cdot b}{d\cdot b}=\dfrac{a \cdot d-c \cdot b}{b \cdot d}\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{a\cdot c}{b \cdot d}\dfrac{a}{b}:\dfrac{c}{d}= \dfrac{a}{b} \cdot \dfrac{d}{c} = \dfrac{a \cdot d}{b \cdot c}\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}= \dfrac{a \cdot d}{b \cdot c} 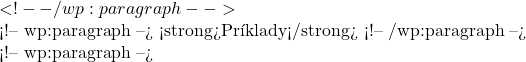\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{1\cdot 3}{2\cdot 3}+ \dfrac{1\cdot 2}{3\cdot 2} =\dfrac{3+2}{6}=\dfrac{5}{6}\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1\cdot 3}{2\cdot 3}- \dfrac{1\cdot 2}{3\cdot 2} =\dfrac{3-2}{6}=\dfrac{1}{6}\dfrac{1}{2}\cdot \dfrac{1}{3}=\dfrac{1 \cdot 1}{2 \cdot 3}=\dfrac{1}{6}\dfrac{1}{2}: \dfrac{1}{3}= \dfrac{1}{2}\cdot \dfrac{3}{1}=\dfrac{3}{2}=1,5 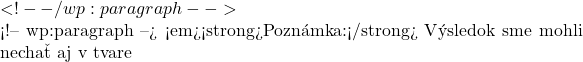\dfrac{3}{2} \dfrac{2}{3}\cdot \left( \dfrac{2}{5}+\dfrac{3}{7}\right)= \dfrac{2}{3}\cdot \dfrac{2 \cdot 7+3\cdot 5 }{5\cdot 7 }= \dfrac{2}{3}\cdot \dfrac{29}{35}=\dfrac{58}{105}\dfrac{1}{3} alebo \dfrac{2}{7}\dfrac{1}{3}=\dfrac{7}{21}\hspace{15} \dfrac{2}{7}=\dfrac{6}{21} \dfrac{1}{3}>\dfrac{2}{7}\dfrac{1}{3}=\dfrac{2}{6}\dfrac{1}{3}>\dfrac{2}{7}$

Poznámka: Výhodou prvého riešenia je, že vieme o koľko je 1/3 väčšia než 2/7, výhodou druhého je, že sme to vypočítali rýchlejšie.

Niekedy stačí, ak výsledok výpočtu zobrazíme na istý počet miest. Výsledok môžeme zaokrúhliť.

Pravidlá zaokrúhľovania:

1. Zaokrúhlenie nadol: Ak prvá číslica, ktorú máme zaokrúhliť je menšia ako 5, predchádzajúce číslice opíšeme a zaokrúhlenú číslicu a všetky číslice za ňou vynecháme.
2. Zaokrúhlenie nahor: Ak prvá číslica, ktorú máme zaokrúhliť je väčšia ako 4, k predchádzajúcej číslici pripočítame jednotku a zaokrúhlenú číslicu a číslice za ňou vynecháme.

Znakom zaokrúhlenia je znak rovná sa a nad ním krúžok alebo bodka:

Continue reading →

Zo skúsenosti vieme, že s rastúcou hĺbkou rastie tlak vody. Od čoho závisí veľkosť tohto tlaku?

Pre tlak platí vzorec:

Na vodu pôsobí gravitačná sila. Stĺpec vody v hĺbke pôsobí silou, ktorá je rovná gravitačnej sile. , kde je hmotnosť stĺpca vody. Continue reading →

Rekurzia v programovaní je, ak procedúra volá samu seba. Aby rekurzia pracovala korektne, parametre, ktoré používa, by mali po nejakom čase dôjsť do stavu, v ktorom sa rekurzia zastaví.

Rekurzia môže byť priama, keď procedúra volá samu seba priamo a môže byť nepriama, ak procedúra vyvolá inú procedúru a táto vyvolá pôvodnú procedúru.

Pomocou rekurzie možno naprogramovať mnohé úlohy výrazne jednoduchšie než bez nej. Continue reading →

Z bežného života poznáte výrazy deciliter, decimeter, centimeter, kilogram, dekagram či v mäsiarstve hovorovo iba deka (prosím si 10 deka šunky). Vo všetkých uvedených prípadoch bola pred fyzikálnu jednotku predradená nejaká predpona. Tieto predpony vyjadrujú násobky alebo diely fyzikálnych jednotiek. Continue reading →

Základné jednotky sústavy SI

(niektoré z nich ste ešte nepreberali) Continue reading →

Na článku sa pracuje

Už pred viac než 2000 rokmi Číňania zistili, že magnet, ak sa môže voľne otáčať, ukazuje jedným pólom magnetu na sever a druhým na juh.

Keďže tú časť magnetickej strelky kompasu ktorá ukazuje na sever, sme nazvali severný magnetický pól a ktorá ukazuje na juh,  južný magnetický pól a rovnaké magnetické póly sa odpudzujú a opačné priťahujú,  na severnej pologuli sa nachádza južný magnetický pól Zeme a na južnej sa nachádza severný magnetický pól Zeme. Pozri obrázok vľavo. V skutočnosti sa magnetické póly Zeme nenachádzajú presne na severnom a južnom póle, sú mierne posunuté. Túto skutočnosť schematicky znázorňuje obrázok vpravo (čierna priamka je os otáčania Zeme, modrá pramka je spojnica medzi severným a južným geomagnetickým pólom). Continue reading →